Задача 31884 Провести полное исследование функции и...

bolanebyla

2018-12-13 03:27:05

Провести полное исследование функции и построить ее график

sova

2018-12-13 12:56:03

★

Область определения (- ∞ ;-2) U (-2;2) U(2;+ ∞ )

y`= ((x^3)`*(x^2-4)-x^3*(x^2-4)`)/(x^2-4)^2

y`=((3x^2*(x^2-4)-x^3*(2x))/(x^2-4)^2

y`=(x^4 -12x^2)/(x^2-4)^2

y`=0

x^4 - 12x^2=0
x^2*(x^2-12)=0 ⇒
x^2 = 0 или x^2=12
x=0 или х = ± 2sqrt(3)

Знак производной:
__+___ (-2sqrt(3)) _-_ (-2) __-__ (0) _-__ (2) __-__ (2sqrt(3)) __+__

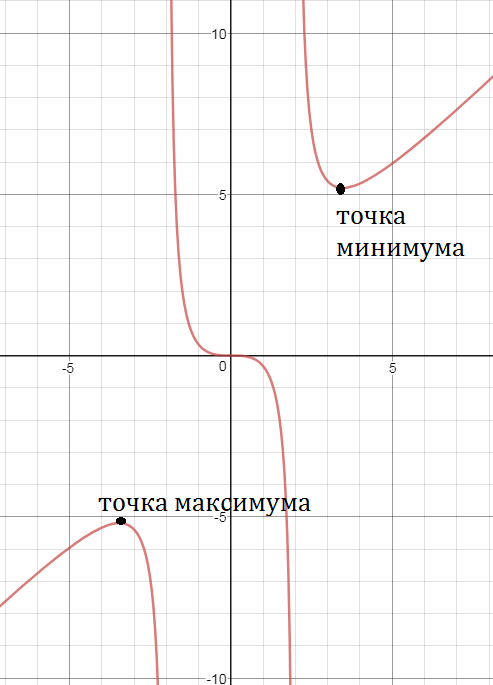
Функция монотонно убывает на (-2sqrt(3); - 2) и на (-2; 2 ) и на (2; 2sqrt(3))
Функция монотонно возрастает
на (- ∞ ;-2sqrt(3)) и на (2sqrt(3);+ ∞ )

x=-2sqrt(3) - точка максимума
f(-2sqrt(3))=(-2sqrt(3))^2/((-2sqrt(3))^2-4)= -3sqrt(3)

х=2sqrt(3) - точка минимума
f(2sqrt(3))=(2sqrt(3))^2/((2sqrt(3))^2-4)= 3sqrt(3)