Задача 31743 Пожалуйста!!! Провести полное...

vk221597205

9 декабря 2018 г. в 20:53

Пожалуйста!!!
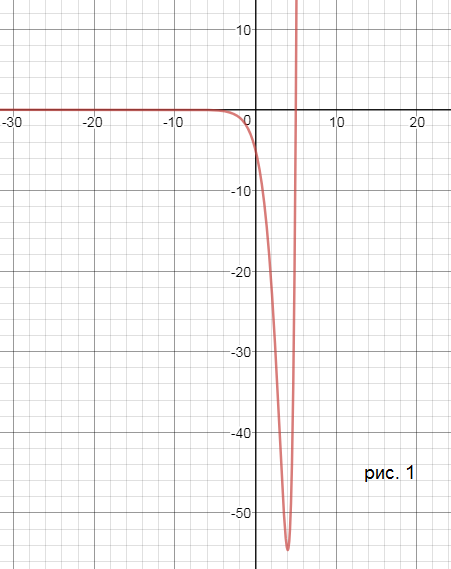
Провести полное исследование функции и построить график

sova

9 декабря 2018 г. в 21:38

★

а)
Область определения (– ∞ ;+ ∞ )
y`=(x–5)`·e^x+(x–5)·e^x=
=1·e^x+(x–5)·e^x=
=e^x·(1+x–5)=
=e^x·(x–4)

y`=0

x–4=0
x=4
Знак производной
__–__ (4) ____ +

y`< 0 на (– ∞ ; –4), функция убывает
y` >0 на (–4; + ∞), функция возрастает

х=4 – точка минимума, производная меняет знак с – на +
y(4)=–e⁴

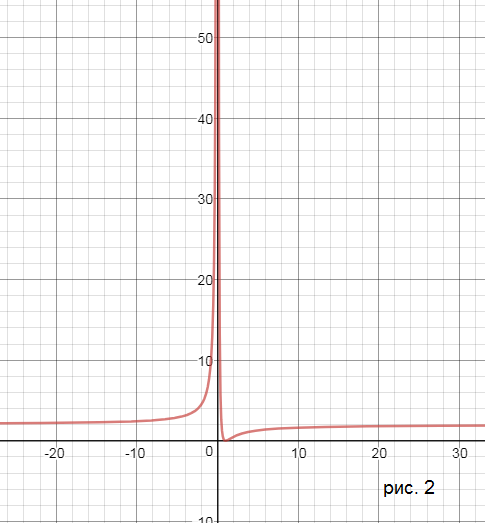
б)
Область определения (– ∞ ;0)U(0;+ ∞ )
y`=2·(((x–1)/x)<sup>2</sup>)`=4·((x–1)/x)·((x–1)/x)`=

=(4(x–1)/x)·((1·x–1·(x–1))/x²)=4(x–1)/x³

y`=0

x–1=0

x=1

Знак производной:

__+__ (0) ___–__ (1) ___+__

y`< 0 на (0 ; 1); функция убывает
y` >0 на (– ∞;0) и на (1;+ ∞); функция возрастает

х=0 – не входит в область определения,
является точкой разрыва 2 рода

Прямая х=0 – вертикальная асимптота
lim_x→2 f(x)=+ ∞

х=1 – точка минимума, производная меняет знак с – на +

Прямая y=2 – горизонтальная асимптота,
lim_{x→ ∞}f(x)=2