Задача 31581 sqrt(2cos^2x-sqrt(2))+sqrt(2)sinx = 0,...
Условие
Решение
{2cos^2x-sqrt(2) ≥ 0 ⇒2*cos^2x ≥ sqrt(2) ⇒ 1+cos2x≥ sqrt(2) ⇒
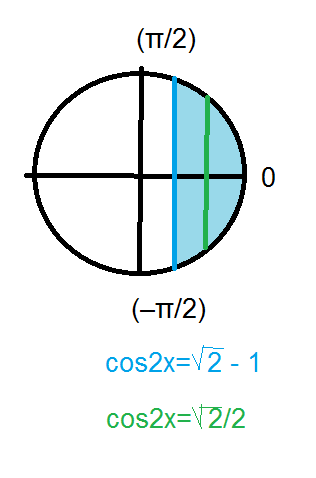
[b]cos2x ≥ sqrt(2) -1[/b]
Перепишем уравнение :
sqrt(2cos^2x-sqrt(2))=-sqrt(2)*sinx
1)
Если sinx > 0
уравнение не имеет корней
2)
Если sinx ≤0
Возводим в квадрат
2cos^2x-sqrt(2)=2sin^2x
2*(cos^2x-sin^2x=sqrt(2)
2cos2x =sqrt(2)
cos2x = sqrt(2)/2
[b]sqrt(2)/2 > sqrt(2)-1[/b]
значит корни
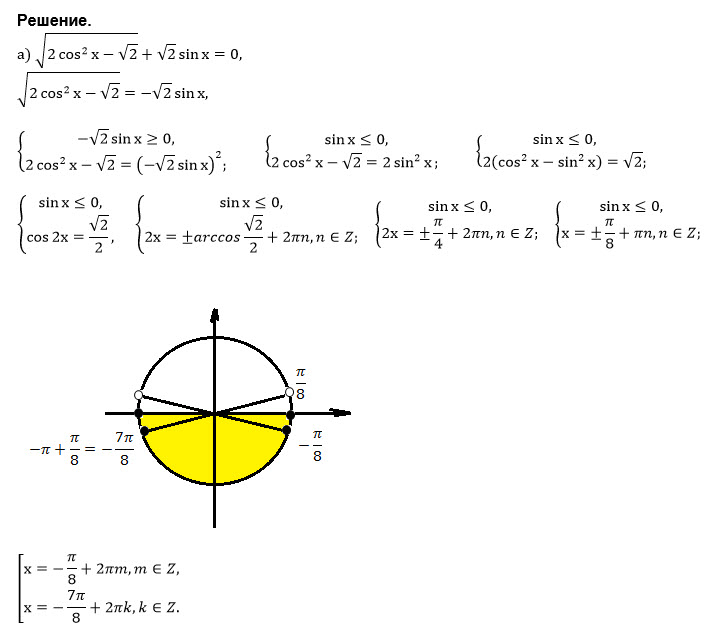
2х= ± ( π/4)+2πn, n ∈ Z - удовлетворяют ОДЗ ( см. рис. 1)
х=± ( π/8)+πn, n ∈ Z
С учетом sinx ≤0
[b]x= (-π/8)+2πk, k ∈ Z
или
х=(-7π/8)+2πm, m ∈ Z [/b]
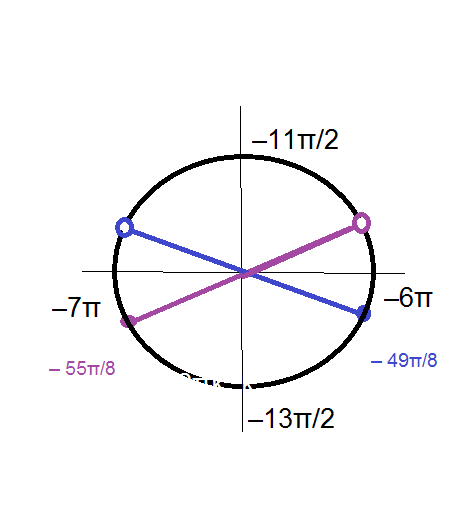
б) Указанному отрезку принадлежат корни:
x_(1)=(-7π/8)-6π= - 55π/8
x_(2)=(-π/8)-6π= - 49π/8
О т в е т.
а) (-π/8)+2πk, (9π/8)+2πm, k, m ∈ Z
б)- 55π/8; - 49π/8
Все решения