Задача 3155 ...

,erbyfjr

07.05.2015

Решите уравнение: sin 2x = 2 cos2 x. Найдите решение на отрезке [-0,5π;1,5π].

Решение смотрите тут: [b][link=https://reshimvse.com/zadacha.php?id=27775][/b]

slava191

07.05.2015

sin2x = 2 cos 2x
2sinxcosx= 2 (cos^2x-sin^2x)
sinxcosx= cos^2x - sin^2x
cos^2x - sinxcosx - sin^2x = 0 делим на sin^2x
tg^2x - ctgx - 1 = 0

SOVA

21.05.2018

sin2x = 2 cos 2x
2sinxcosx= 2 (cos^2x–sin^2x)
sinxcosx= cos^2x – sin^2x
sin^2x + sinxcosx – cos^2x = 0 - однородное тригонометрическое уравнение, делим на cos^2x
tg^2x +tgx – 1 = 0
Квадратное уравнение относительно tgx
D=1+4=5
корни
(-1-sqrt(5))/2 или (-1+sqrt(5))/2

tgx=(-1-sqrt(5))/2
x=arctg((-1-sqrt(5))/2)+ Pik, k - целое
или
tgx=(-1+sqrt(5))/2
x=arctg((-1+sqrt(5))/2)+ Pin, n - целое

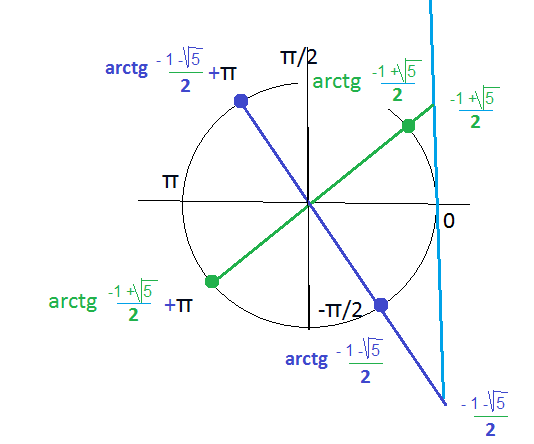
Указанному отрезку принадлежат корни
arctg((-1-sqrt(5))/2);
arctg((-1+sqrt(5))/2);
arctg((-1-sqrt(5))/2)+Pi;
arctg((-1+sqrt(5))/2)+Pi;