Задача 31122 а) Решить уравнение...

lolokek

2018-11-18 16:18:50

а) Решить уравнение 2sin(x+Pi/6)-2sqrt(3)cos^2x = cosx-2sqrt(3)

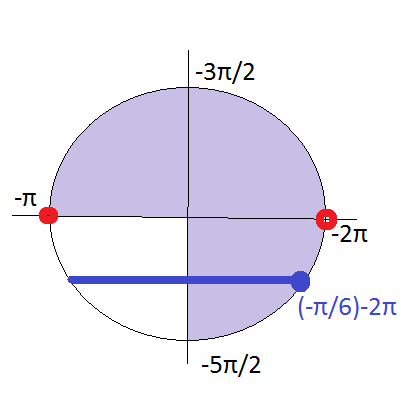
б) Отобрать корни на отрезке [-5Pi/2; -Pi]

sova

2018-11-18 16:31:03

По формуле синуса суммы

sin(х +(π/6))=sinх*cos(π/6)+cosх*sin(π/6)=(sqrt(3)sinx+cosx)/2

Уравнение принимает вид

sqrt(3)*sinx+cosx-2sqrt(3)cos^2x=cosx-2sqrt(3)

sqrt(3)*sinx+2sqrt(3)cos^2x=-2sqrt(3)

Так как сos^2x=1-sin^2x

2sqrt(3)sin^2x+sqrt(3)sinx=0

sqrt(3)*sinx*(2sinx+1)=0

sinx=0 ⇒ x=πk,k ∈ Z

или

2sinx+1=0 ⇒ sinx=-1/2 ⇒ x=(-1)^(n+1)*(π/6)+πn, n ∈ Z

О т в е т.
а) πk,k ∈ Z

(-1)^(n+1)*(π/6)+πn, n ∈ Z

б) -π; -2π; (-π/6)-2π=-13π/6 три корня, принадлежащих указанному промежутку