Задача 29949 sinx=sqrt((1-cosx)/2), [2Pi; 7Pi/2]...
Условие
Решение
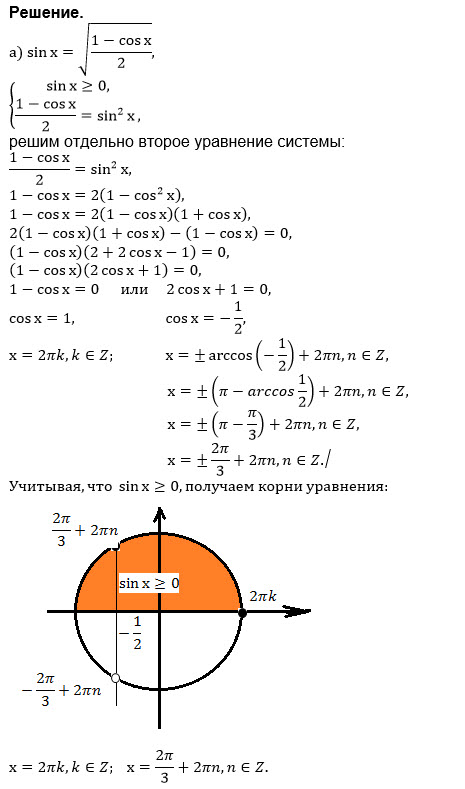
Если sinx ≥ 0, возводим в квадрат (подкоренное выражение неотрицательно при любом х)
{sinx ≥ 0
{sin^2x=(1-cosx)/2
sin^2x=1-cos^2x
1-cos^2x=(1-cosx)/2
(1-cosx)*(1+cosx) -(1-cosx)/2=0
(1-cosx)*(1+cosx-(1/2))=0
(1-cosx)*((1/2)+cosx)=0
1-cosx=0 или сosx +(1/2)=0
Решаем первое уравнение
1-cosx=0
cosx=1
x=2πk, k ∈ Z
Решаем второе уравнение
cosx= - (1/2)
x= ± ( 2π/3)+2πn, n ∈ Z
Условию sinx ≥ 0 удовлетворяют х=( 2π/3)+2πn, n ∈ Z
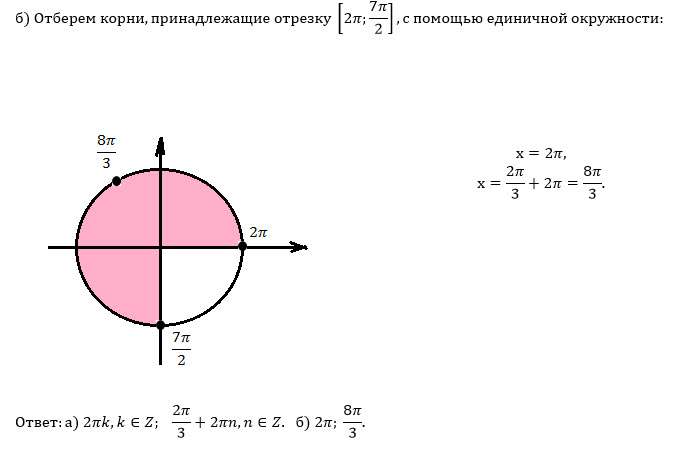
Указанному отрезку принадлежат корни:
x_(1)=2π
x_(2)=( 2π/3)+2π=8π/3
О т в е т.
2πk, k ∈ Z; ( 2π/3)+2πn, n ∈ Z
{2π; 8π/3} ∈ [2π; 7π/2]
Все решения