Задача 29496 ...

slava191

7 сентября 2018 г. в 00:35

а) Решите уравнение 20^cosx=4^cosx⋅5^−sinx.

б) Найдите все корни этого уравнения, принадлежащие отрезку [−9π/2;−3π].

sova

9 сентября 2018 г. в 12:00

20^cosx=(4·5)^cosx=4^cosx·5^cosx

4^cosx·5^cosx=4^cosx·5^–sinx

4^cosx > 0 при любом х, показательная функция принимает только положительные значения.

5^cosx=5^–sinx ⇒ cosx=–sinx ⇒ tgx=–1

x=(–π/4)+πk, k ∈ Z

О т в е т. а) (–π/4)+πk, k ∈ Z

б) Корни уравнения
в 4–ой
((–π/4)+2πn, n∈ Z )
и
во 2–ой
(3π/4)+2πn, n∈ Z )
четвертях.
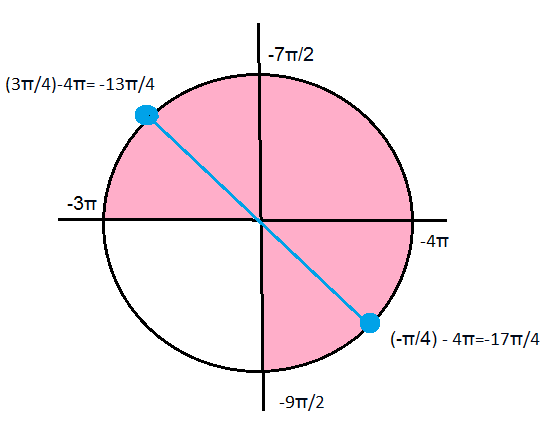
Чтобы отобрать принадлежащие указанному промежутку, рассматриваем единичную окружность ( см. рис.)

Указанному промежутку принадлежат корни

x₁= (–π/4)–4π=–17π/4;
x₂=(3π/4)–4π=–13π/4

О т в е т. б) –17π/4; –13π/4