Задача 29171 ...
Условие
Решение
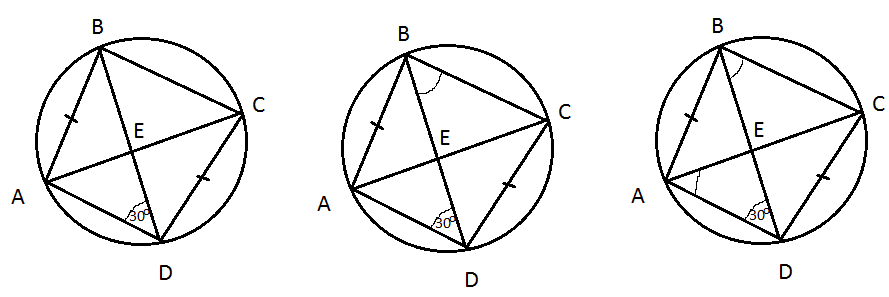
Так как АВ=CD, то ∪АВ=∪ СD
Cледовательно, ∠ВDA=∠СВD, как вписанные углы, опирающиеся на равные дуги.
В четырехугольнике АВСD
∠ВDA и ∠СВD – внутренние накрест лежащие углы, значит
AD|| BC и ABCD – равнобедренная трапеция.
Так как ∠САD=∠СВD, как вписанные углы, опирающиеся на одну и ту же дугу.
∠СВD=∠ВDA=30°, то ∠САD=30° .
Тогда из треугольника АЕD, cумма углов которого равна 180°, находим
∠АЕD=180°-∠САD -∠ВDA= 180° - 30°- 30°=180° - (30°+ 30°)=120°
В равнобедренной трапеции АВСD диагонали равны
BD=AC=20
S(трапеции ABCD)= (1/2)∙AC∙BD∙sin∠АЕD =(1/2)∙20∙20∙sin 120°=100√3
О т в е т. 100√ 3
Ответ: 100√ 3
