Задача 28180 Решите пожалуйста ...
Условие
534
Решение
★
log_(a)x=b ⇒ х=a^b
2^(2x)-sqrt(3)cosx-sin2x=4^x
так как
2^(2x)=4^x,
то
-sqrt(3)cosx-sin2x=0
sin2x=2sinx*cosx (формула синуса двойного угла)
-sqrt(3)cosx-2sinx*cosx=0
-cosx*(sqrt(3)+2sinx)=0
cosx=0 или sqrt(3)+2sinx=0
сosx=0 ⇒ x=(Pi/2)+Pin, n ∈ Z
или
sinx=-sqrt(3)/2 ⇒ x=(-1)^(k)arcsin(-sqrt(3))/2)+Pik, k ∈ Z
x=(-1)^(k)*(-Pi/3)+Pik, k ∈ Z
О т в е т.
x=(Pi/2)+Pin, n ∈ Z
(-1)^(k)*(-Pi/3)+Pik, k ∈ Z
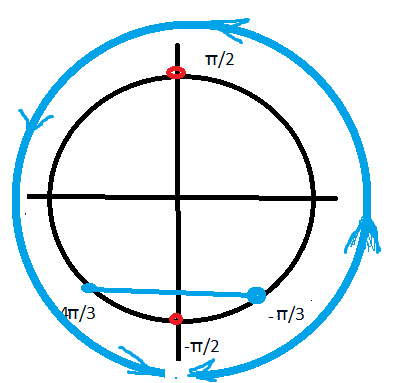
Отрезку [-Pi/2; + 3Pi/2] принадлежат корни
-Pi/2; +Pi/2; 3Pi/2;
-Pi/3 и (-2Pi/3)+2Pi=4Pi/3
.
