Задача 27973 Окружности радиусов 2 и 3 с центрами O1...
Условие
Перерешиваем: [link=https://reshimvse.com/zadacha.php?id=536]
Решение
Значит
∠ АВО_(1)= ∠ О_(1)АВ=30^(o)
∠ BO_(1)A=120^(o)
По теореме косинусов
АВ^2=r^2+r^2-2*r*r*cos120^(o)=4+4-2*4*(-1/2)=12
AB=2 sqrt(3)
Или высота равнобедренного треугольника, проведенная из вершины O_(1) на сторону АВ, делит АВ пополам.
Поэтому
(1/2) АВ=r*cos30^(o) ( все верно в 536)
AB=2r*cos30^(o)
Аналогично
Треугольник АО_(2)В- равнобедренный (ВО_(2)=АО_(2)=R=3)
∠CАО_(2)=∠ ВAО_(1) как вертикальные
Значит ∠ АСО_(2)= ∠ О_(2)АС=30^(o)
∠ СO_(2)A=120^(o)
По теореме косинусов
АС^2=R^2+R^2-2*R*R*cos120^(o)=9+9-2*9*(-1/2)=27
AC=3 sqrt(3)
Или как верно написано в решении 536
АС=2R*cos 30 градусов=3*sqrt(3)
Или из подобия треугольников
АО_(1)B и СО_(2)А
AC/BC=R/r
AC=(3/2)*BC=3sqrt(3)
BC=BA+AC=2 sqrt(3)+3sqrt(3)=5sqrt(3)
S( Δ BCO_(2))=(1/2)*BC*CO_(2)*sin30^(o)=(1/2)*5sqrt(3)*3*(1/2)=15sqrt(3)/4
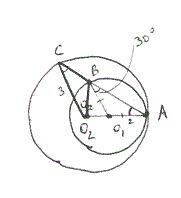
Второй случай расположения окружностей.
Решение аналогично предыдущему.
Треугольник АО_(1)В- равнобедренный (ВО_(1)=АО_(1)=r=2)
Значит
∠ АВО_(1)= ∠ О_(1)АВ=30^(o)
∠ BO_(1)A=120^(o)
По теореме косинусов
АВ^2=r^2+r^2-2*r*r*cos120^(o)=4+4-2*4*(-1/2)=12
AB=2 sqrt(3)
Или высота равнобедренного треугольника, проведенная из вершины O_(1) на сторону АВ, делит АВ пополам.
Поэтому
(1/2) АВ=r*cos30^(o) ( все верно в 536)
AB=2r*cos30^(o)
Аналогично
Треугольник АО_(2)В- равнобедренный (ВО_(2)=АО_(2)=R=3)
∠CАО_(2)=∠ ВAО_(1) как вертикальные
Значит ∠ АСО_(2)= ∠ О_(2)АС=30^(o)
∠ СO_(2)A=120^(o)
По теореме косинусов
АС^2=R^2+R^2-2*R*R*cos120^(o)=9+9-2*9*(-1/2)=27
AC=3 sqrt(3)
BC=AC-AB=3 sqrt(3)-2sqrt(3)=sqrt(3)
и потому
S( Δ BCO_(2))=(1/2)*BC*CO_(2)*sin30^(o)=(1/2)*sqrt(3)*3*(1/2)=3sqrt(3)/4
О т в е т. 15 sqrt(3)/4 или 3sqrt(3)/4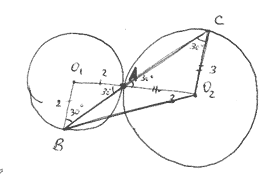
Все решения
