Задача 536 Окружности радиусов 2 и 3 с центрами O1...
Условие
математика 10-11 класс
9847
Решение
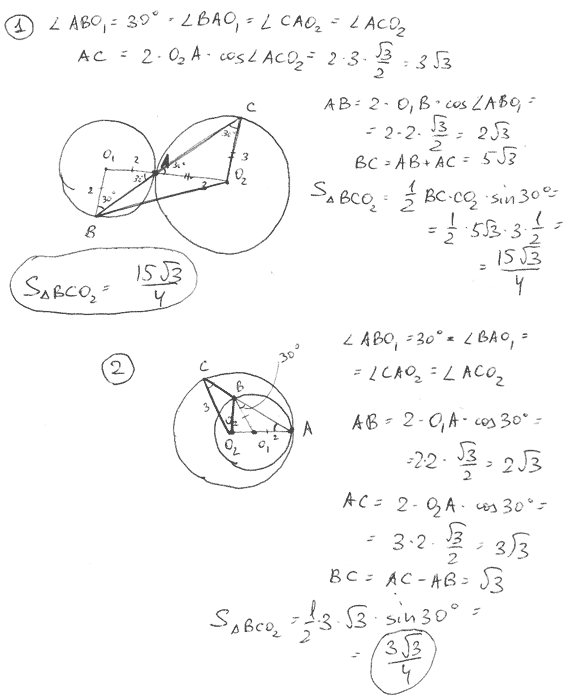
Ответ: 15*sqrt(3)/4 и 3*sqrt(3)/4

Ответ: 15*sqrt(3)/4 и 3*sqrt(3)/4