Задача 26526 1.27 2.27 3.27 4.27...
Условие
2.27
3.27
4.27
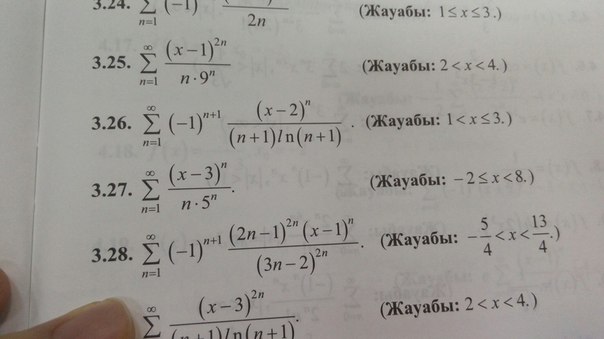


предмет не задан
1602
Все решения
R=lim_(n→∞)a_(n)/a_(n+1)=
=lim_(n→∞)((n+1)^2*2^(n+1))/((n+2)^2*2^n)=2
(-2;2) - интервал сходимости
При х=2 и х=-2 числовые ряды ∑^(+∞)_(1) (n+1)^2 и ∑^(+∞)_(1) (-1)^n(n+1)^2 расходятся
О т в е т. (-2;2) - область сходимости
3)
Применяем признак Даламбера
R=lim_(n→∞)a_(n)/a_(n+1)=
=lim_(n→∞)(5^(n+1)*(n+1))/(n*5^(n))=5
|x-3| < 5
-5 < x-3 < 5
-2 < x < 8
(-2;8) - интервал сходимости
При х= 8 числовой ряд ∑^(+∞)_(1) *(1/n) расходится . Это гармонический ряд
При х= - 2 числовой ряд ∑^(+∞)_(1) (-1)^n1(1/n) сходится
по признаку Лейбница.
|a_(n)|→0 и (1/n) монотонно убывает
О т в е т. [-2;8) - область сходимости
