Задача 26077 Провести полное исследование функции и...
Условие
1. найти область определения функции
2. определить четность и периодичность
3. найти точки пересечения с началом координат
4. найти асимптоты (если есть)
5. найти интервалы монотонности и экстремумы (если есть)
6. найти интервал выпуклости, интервал и точки перегиба
7. найти дополнительные точки
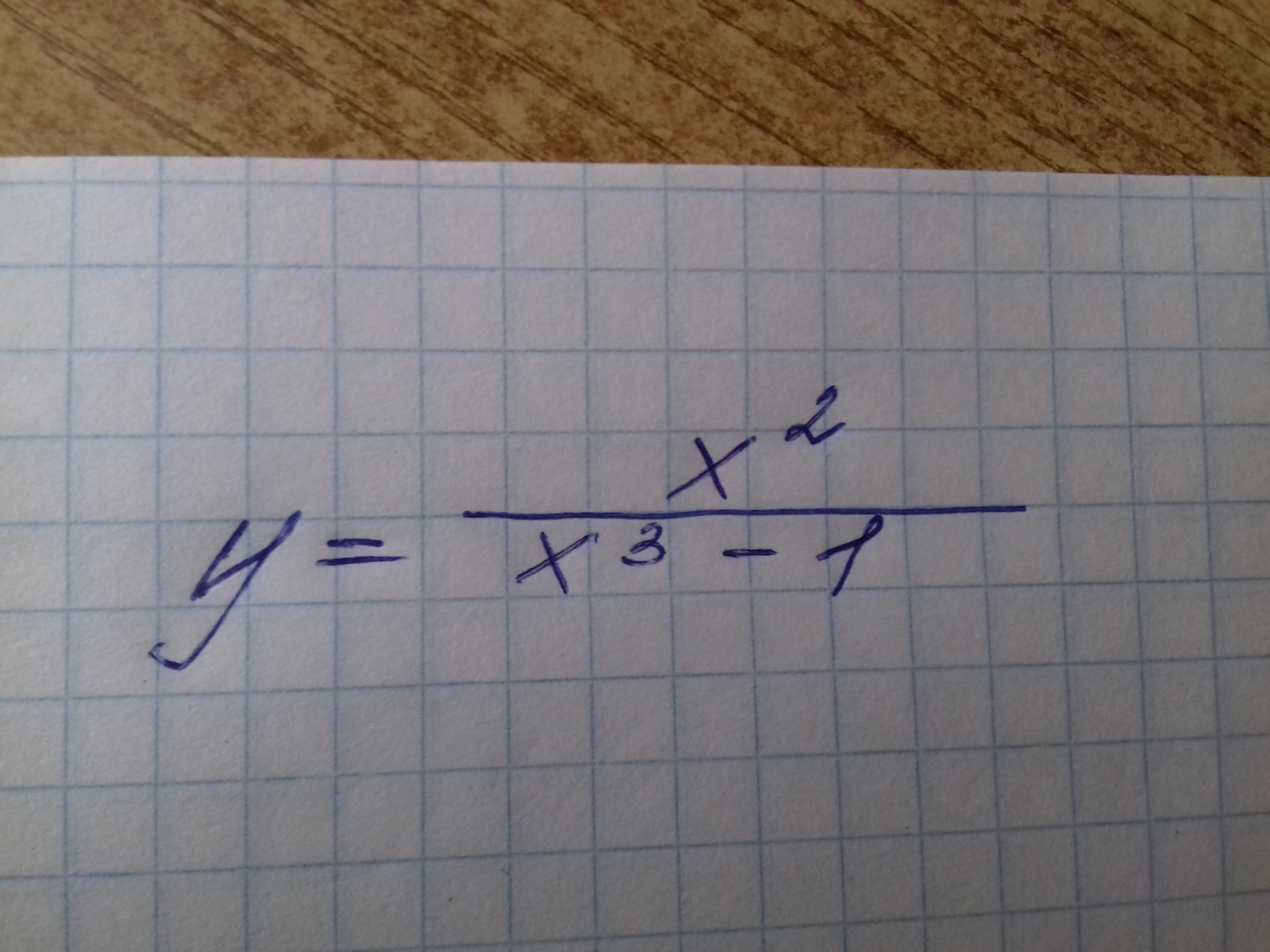
Решение
(-бесконечность;1)U(1;+бесконечность)
2. Функция не является ни четной, ни нечетной, так как
y(-x)=(-x)^2/((-x)^3-1) =x^2/(-x^3-1)
y(-x) ≠ y(x)
y(-x) ≠ -y(x)
3. Точки пересечения с осями координат
y=0 ⇒ x=0
(0;0)- точка пересечения и осью Ох и с осью Оу.
4. Асимптоты
x=1 - вертикальная асимптота
lim_(x→1-0)= - ∞
lim_(x→1+0)= + ∞
y=0 - горизонтальная асимптота
lim_(x→∞)=0
5.Интервалы монотонности и экстремумы
y`=((x^2)`*(x^3-1)-(x^3-1)`*x^2)/(x^3-1)^2
y`=(-x^4-2x)/((x^3-1)^2
y`=0
-x^4-2x=0
x*(-x^3-2)=0
x=0 или х=∛-2
Расставляем знак производной:
_-__ (∛-2) _+__ (0) _-__ (1) _-__
х= ∛-2 - точка минимума, производная меняет знак с - на +
х=0 - точка максимума, производная меняет знак с + на -
Функция возрастает на (∛-2;0)
убывает на ( - бесконечность; ∛-2) и на (0;1) и на (1;+ бесконечность)
6.Интервал выпуклости, точки перегиба
y``=((-x^4-2x)`*(x^3-1)^2 - ((x^3-1)^2)`*(-x^4-2x))/(x^3-1)^4
y``=(2x^6+14x^3+2)/(x^3-1)^3
y``=0 ⇒ 2x^6+14x^3+2=0 D=196-4*2*2=180
x^3=(-14-sqrt(180))/4 или x^3=(-14+sqrt(180))/4
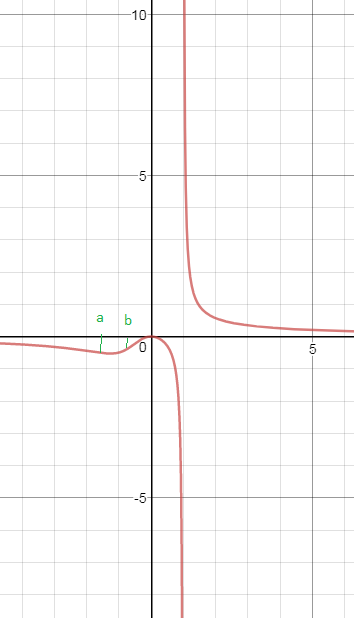
Две точки перегиба
(отмечены на рисунке).
a= ∛ (-14-sqrt(180))/4 и b= ∛(-14+sqrt(180))/4
Кривая выпукла вверх на (-бесконечность;∛ (-14-sqrt(180))/4 )
и на (∛(-14+sqrt(180))/4; 1)
Кривая выпукла вниз на (∛ (-14-sqrt(180))/4; ∛(-14+sqrt(180))/4) и на (1;+ бесконечность)
7.
x=2 y=4/7
x=4 y=16/63
x=-2 y=-4/9