Задача 23903 Наудачу взяты два положительных числа х...

slava191

18.02.2018

Наудачу взяты два положительных числа х и y,каждое из которых не превышает единицы. Найти веро­ятность того, что сумма x+у не превышает единицы, а произведение xy не меньше 0,09.

SOVA

18.02.2018

★

Пусть Х и У - выбранные числа, их возможные значения
0 меньше или равно Х меньше или равно 1
0 меньше или равно У меньше или равно 1
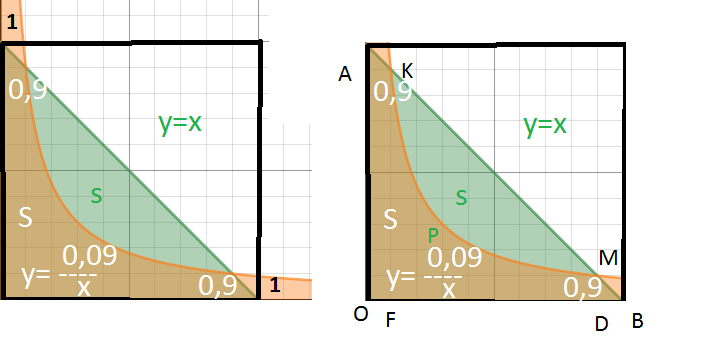
Геометрическая интерпретация указанной области - квадрат со сторонами 1.
S=S(квадрата)=1
Благоприятствующие условия - попадание Х и У в область
OТКРMD, определяемую системой неравенств
{x+y меньше или равно 1
{xy меньше или равно 0,09
{0 меньше или равно x меньше или равно 1
{0 меньше или равно y меньше или равно 1

Найдем координаты точек К и М.
{x+y=1 ⇒ y=1-x
{y=0,09/x

1-x=0,09/x
x^2-x+0,09=0
D=1-4*0,09=1-0,36=0,64
x_(К)=0,1 y_(K)=0,9
x_(M)=0,9 y_(M)=0,1

S(FКРMD)= S( трапеции KMDF)- S ( криволин. треуг. КРМ)=

=(1/2)*((KF+MD)*FD/2)- ∫^(0,9) _(0,1)(0,09/x)dx=

= ((0,9+0,1)*0,8/2)-(0,09lnx)|^(0,9) _(0,1)=

=0,4-0,09*(ln0,9-ln0,1)=0,4-0,09*ln9=

=0,4 - 0,18ln3=0,4 - 0,197750... ≈ 0,20225

p=mes( Δ ОАКPMB)/mes(квадрата со стороной 1)≈0,20225/1=0,20225