Задача 2280 В прямоугольном треугольнике угол между...

slava191

23.11.2014

В прямоугольном треугольнике угол между высотой и медианой, проведёнными из вершины прямого угла, равен 28 градусов. найдите больший из острых углов треугольника

||| Вариант решения 1. |||

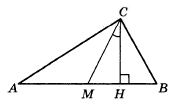
1) Высота, проведенная из вершины прямого угла, делит треугольник на два подобных треугольника между собой и подобных данному. Из подобия треугольников АВС и НСВ следует: В=НСА.

2) Медиана, проведенная из вершины прямого угла, равна половине гипотенузе. Значит треугольник МВС - равнобедренный, и ВСН=В=НСА.

3) НСА+ВСН=90о-МСН=90 градусов-28 градусов=62; НСА=62/2=31.

4) А=90-НСА=90-31=59.

||| Вариант решения 2. |||

Ответ: 59