Задача 21938 а) Решите уравнение...

slava191

02.01.2018

а) Решите уравнение cos^25x+2cos5xsin(x-Pi/10)+1=0

б) Найдите решения уравнения, принадлежащие промежутку [2016Pi; 2017Pi].

SOVA

02.01.2018

★

cos5x=a
sin(x-(Pi/10))=b
a^2+2a*b+1=a^2+2ab+b^2-b^2+1
Прибавим и вычтем
sin^2(x-(Pi/10))

Выделим полный квадрат
(сos5x+sin(x-(Pi/10))^2+1-sin^2(x-(Pi/10))=0

Так как
1-sin^2(x-(Pi/10))=сos^2((x-(Pi/10))

уравнение принимает вид
(сos5x+sin(x-(Pi/10))^2+cos^2(x-(Pi/10))=0

Cумма двух неотрицательных выражений равна 0 тогда и только тогда, когда каждое из них равно 0
{сos5x+sin(x-(Pi/10))=0
{cos(x-(Pi/10))=0
Решаем первое уравнение:
Так как
cos5x=sin((Pi/2)-5x), то

sin((Pi/2)-5x)+sin(x-(Pi/10))=0
2*sin((2Pi/10)-2x)*cos((3Pi/10)-3x)=0

sin((2Pi/10)-2x)=0 или cos((3Pi/10)-3x)=0
Используем свойство нечетности синуса и четности косинуса

-sin(2х-(2Pi/10))=0 ⇒ 2х-(2Pi/10)=Pik, k ∈ Z ⇒
2x=(Pi/5)+Pik, k ∈ Z ⇒ x=(Pi/10)+(Pi/2)*k, k ∈ Z

cos(3x-(3Pi/10))=0 ⇒ 3х-(3Pi/10)=(Pi/2)+Pin, n ∈ Z ⇒
3x=(3Pi/10)+(Pi/2)+Pim, m ∈ Z ⇒
x=(Pi/10)+(Pi/6)+(Pi/3)*m, m ∈ Z ⇒
x=(4Pi/15)+(Pi/3)*m, m ∈ Z

Решаем второе уравнение
cos(x-(Pi/10))=0
x-(Pi/10)=(Pi/2)+Pin, n ∈ Z
⇒ х=(Pi/10)+(Pi/2)+Pin, n ∈ Z
х=(6Pi/10)+Pin, n ∈ Z

Решение системы
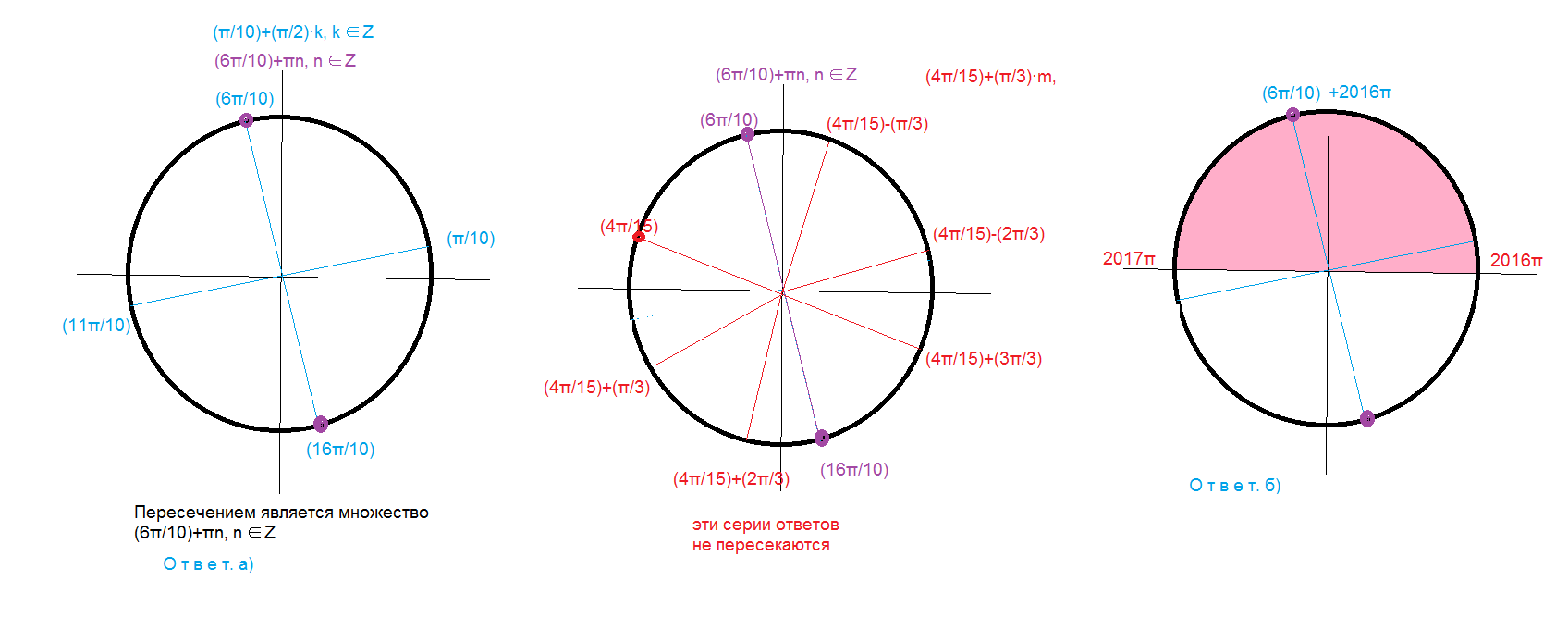
{ x=(Pi/10)+(Pi/2)*k, k ∈ Z или =(4Pi/15)+(Pi/3)*m, m ∈ Z
{x=(6Pi/10)+Pin, n ∈ Z

О т в е т а).(6Pi/10)+Pin, n ∈ Z

б) Указанному промежутку принадлежат корни
2016Pi < (6Pi/10)+Pin < 2017Pi
2016 < (6/10)+n < 2017
20160 < 6+10n < 20170
20154 < 10n < 20164
n=2016

(6Pi/10)+Pi*2016=(20166/10)Pi ∈ [2016π; 2017π]