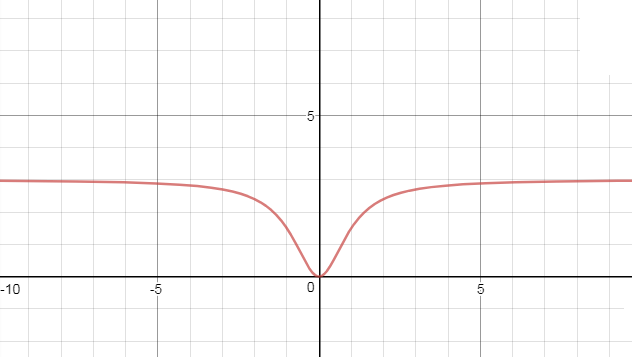
Задача 21832 Провести исследование и построить график...
Условие

Решение
Вертикальных асимптот нет
2) Функция является четной.
у(–х)=3(–х)^2/((–x)^2+1)=3x^2/(x^2+1)
y(–x)=y(x)
3)limx→ +∞)f(x)=+3
limx→–∞f(x)=+3.
y=3 - горизонтальная асимптота
Наклонной асимптоты нет, так как
k=limx→∞(f(x))/x=0
4) Точки пересечения с осями координат
С осью ОХ
f(x)=0
3x^2/(x^2+1)=0
x^2=0
x=0
C осью Оу
х=0 ⇒ у=0
(0;0) – точка пересечения с осью Ох и с осью Оу.
5)
y`=((3x^2)`*(x^2+1)-(x^2+1)`*(3x^2))/(x^2+1)^2;
y`=6x/(x^2+1)
y`=0
6x=0
x=0
Знак производной
_–__ (0) ___+___
x=0 – точка минимума, производная меняет знак с – на +
Функция убывает при x∈ (–∞;0) и
возрастает при x∈ (0;+∞)
у(0)=0 - наименьшее значение функции
6)y``=(6x)`(x^2+1)^2-((x^2+1)^2)`*6x)/(x^2+1)^4=
=(6-18x^2)/(x^2+1)^3
y``=0
6-18x^2=0
x= ± √(1/3) –точки перегиба, вторая производная при переходе через точки меняет знак .
Функция выпукла вверх на (– ∞ ;–√(1/3)) и на (√(1/3);+ ∞ )
выпукла вниз на (–√(1/3);√(1/3))