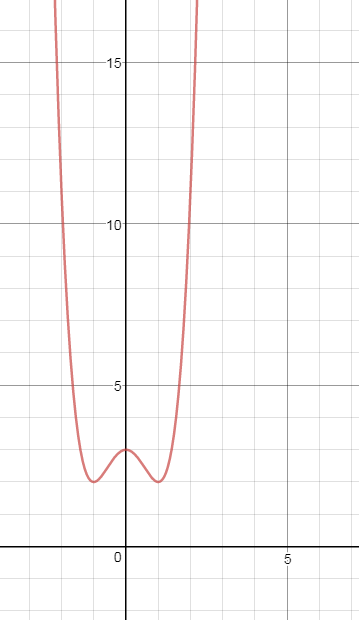
Задача 21828 Провести исследование и построить график...

vk340246274

27.12.2017

Провести исследование и построить график y=x^4-2x^2+3

SOVA

28.12.2017

★

1) D(y)=(–∞;+ ∞)
Вертикальных асимптот нет

2) Функция является четной.
у(-х)=(-х)^4-2*(-x)^2+3=x^4-2x^2+3
y(-x)=y(x)

3)lim_(x→ +бесконечность))f(x)=+бесконечность
lim_(x→-бесконечность)f(x)=+бесконечность.

Горизонтальных асимптот нет

Наклонной асимптоты нет, так как
k=lim_(x→бесконечность)(x^4-2x^2+3)/x=+бесконечность

4) f(x)=0
x^4-2x^2+3=0
D=4-4*3 < 0
Точек пересечения с осью Ох нет.

При х=0 у=3
(0;3) - точка пересечения с осью Оу.

5)
y`=4x^3-4x;
y`=0
4x^3-4x=0
4x*(x^2-1)=0
x=0 или x^2-1=0 ⇒х=±1

Знак производной
_-__ (-1) ___+___ (0) __–__ (1 ) __+__


x=0 – точка максимума, производная меняет знак с + на -

x=-1 и х=1 - точки минимума, производная меняет знак с - на +


Функция убывает при x∈ (-бесконечность;-1) и x∈ (0;1)
возрастает при x∈ (-1;0) и (1;+бесконечность)


7)y``=(4x^3-4x)`=12x^2-4
y``=0
12x^2-4=0
x= ± sqrt(1/3) -точки перегиба, вторая производная при переходе через точки меняет знак .

Функция выпукла вниз на (- бесконечность ;-sqrt(1/3)) и на (sqrt(1/3);+ бесконечность )
выпукла вверх на (-sqrt(1/3);sqrt(1/3))