Задача 21707 а) Решите уравнение...

slava191

25.12.2017

а) Решите уравнение cos^2x+4cos^23x+4cos3xcosx-6cosx-12cos3x=-9

б) Найдите решения уравнения, принадлежащие промежутку [2015Pi; 2017Pi]

SOVA

25.12.2017

★

а)
Выделим полный квадрат
cos^2x+4cos^23x+4cos3x*cosx=
=(cosx+2cos3x)^2

Уравнение принимает вид
(cosx+2cos3x)^2-6*(cosx+2cos3x)+9=0
Формула квадрата разности
(cosx+2cos3x-3)^2=0
cosx+2cos3x-3=0
cosx+2cos3x=3
Так как наибольшее значение косинуса 1, то равенство возможно лишь при
{cosx=1
{2cos3x=2

Система
{cosx=1 ⇒ x=2Pik, k ∈ Z
{cos3x=1⇒ 3x=2Pin, n ∈ Z ⇒ x=(2Pi/3)n, n ∈ Z

Решение удовлетворяющее системе
x=2Pik, k ∈ Z
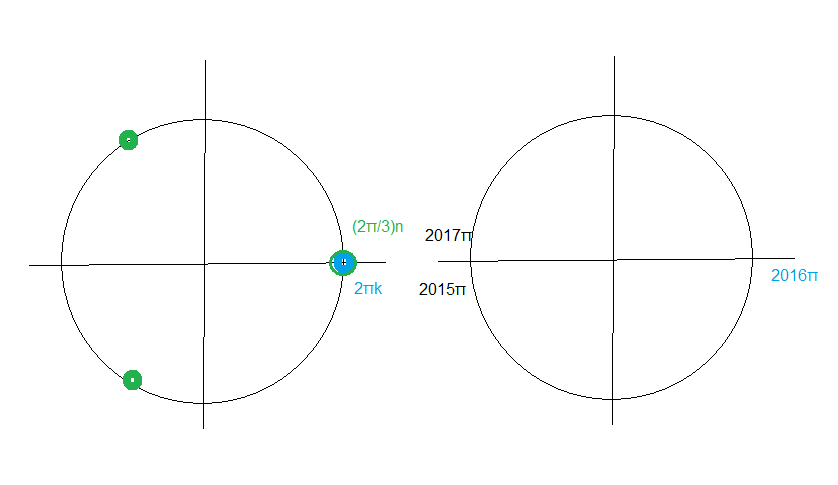
(см. рис.)

б) Указанному промежутку удовлетворяет х=2016Pi


О т в е т. а)2Pik, k ∈ Z; б) 2016Pi