Задача 16861 В треугольной пирамиде PABC с основанием...

slava191

17.07.2017

В треугольной пирамиде PABC с основанием АВС известно, что АВ=17, РВ=10, cosPBA = 32/85. Основанием высоты этой пирамиды является точка С. Прямые РА и ВС перпендикулярны.

а) Докажите, что треугольник АВС прямоугольный

б) Найдите объем пирамиды РАВС.

SOVA

20.07.2017

★

а)
PC- высота пирамиды.
РС ⊥ пл. АВС

ВС- проекция РВ, АС- проекция РА.
По условию РA ⊥ BC, значит по теореме о трех перпендикулярах АС ⊥ ВС.
∠ АСВ=90 градусов, Δ АВС - прямоугольный.
б)
По теореме косинусов из треугольника РАВ:
РА^2=AB^2+PB^2-2*AB*PB*cos ∠PBA=
=17^2+10^2-2*17*10*(32/85)=289+100-128=261

По теореме Пифагора
PA^2=PC^2+AC^2;
PB^2=PC^2+BC^2
AC^2+BC^2=AB^2

261=PC^2+AC^2
100=PC^2+BC^2
Cкладываем
361=2PC^2+AC^2+BC^2, но AC^+BC^2=289

2РC^2=361-289
PC^2=36
PC=6

AC=sqrt(PA^2-PC^2)=sqrt(261-36)=sqrt(225)=15;
BC=sqrt(PB^2-PC^2)=sqrt(100-36)=sqrt(64)=8;

V=(1/3)S(основания)*Н=
=(1/3)*(1/2)*АС*ВС*РС=(1/6)*15*8*6=120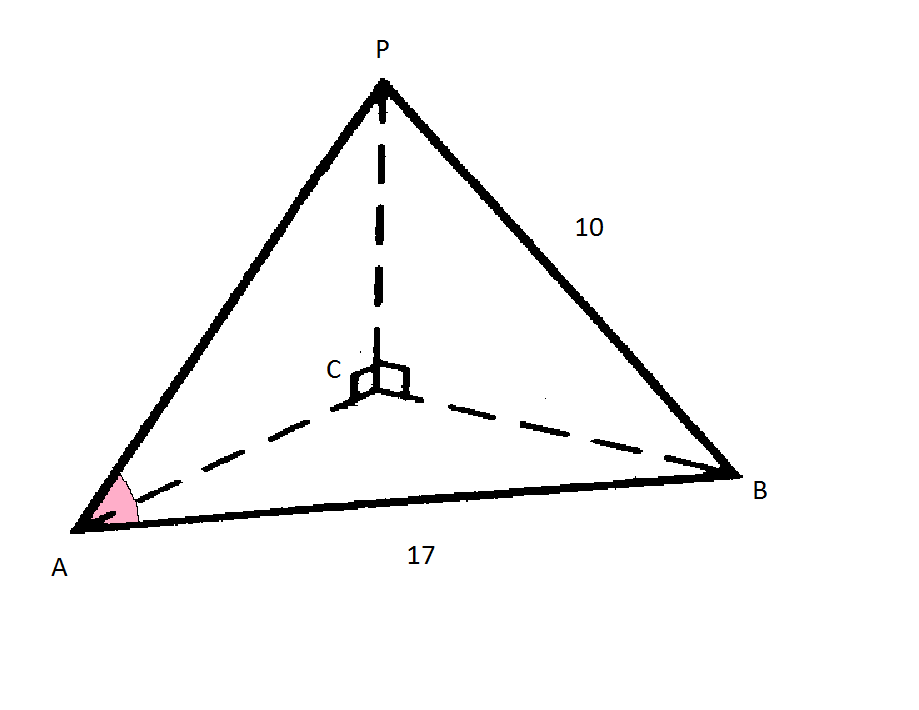

Ответ: 120