Задача 15539 Укажите, какие из следующих утверждений...
Условие
1) Центр окружности, описанной около треугольника, лежит на пересечении его биссектрис.
2) Радиус окружности, вписанной в правильный треугольник, в 2 раза меньше радиуса описанной окружности.
3) Центр окружности, вписанной в равнобедренный треугольник, лежит на высоте, проведенной к основанию.
4) Если треугольник ABC описан около окружности с центром О, то ОА = ОВ = ОС.
Решение
Ответ: 23
Решение
2) Радиус окружности, вписанной в правильный треугольник, в 2 раза меньше радиуса описанной окружности- ВЕРНО, потому что центр описанной около правильного треугольника окружности и центр вписанной в правильный треугольник окружности совпадают.
Центр О - точка пересечения и биссектрис и медиан.
А медианы в точке пересечения делятся в отношении 2:1, считая от вершины.
(см. рисунок)
R:r=2:1
3) Центр окружности, вписанной в равнобедренный треугольник, лежит на высоте, проведенной к основанию - ВЕРНО, так как центр окружности вписанной в любой треугольник- точка пересечения биссектрис.
Высота равнобедренного треугольника является одновременно и медианой и биссектрисой.
4) Если треугольник ABC описан около окружности с центром О, то ОА = ОВ = ОС - НЕВЕРНО.
Это верно для вписанного в окружность треугольника.
О т в е т. 23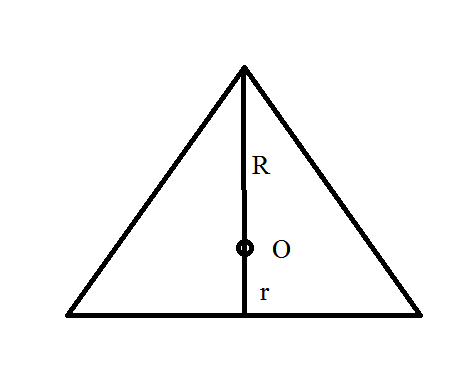
Все решения
