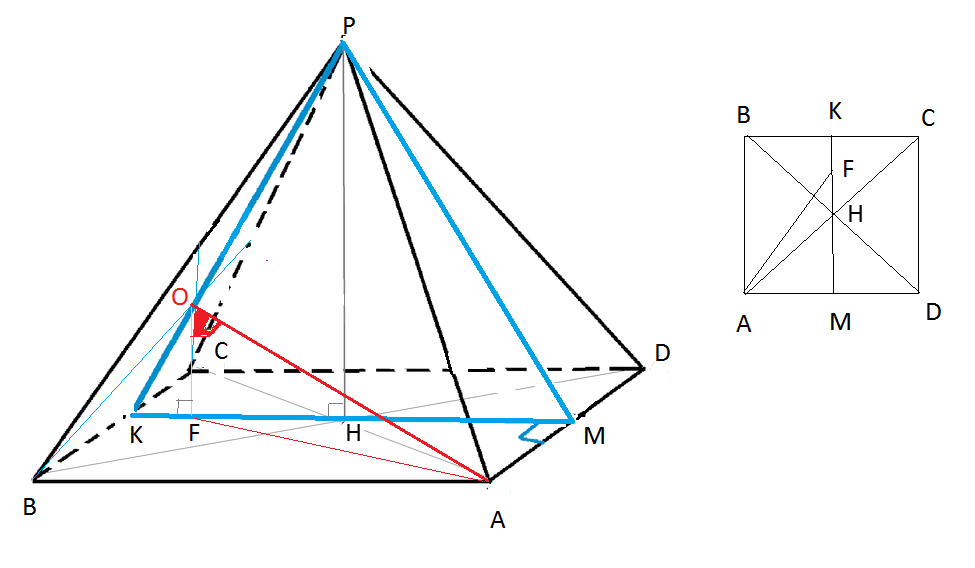
Задача 12098 PH - высота правильной четырехугольной...
Условие
А) Докажите, что прямые РН и АО не имеют общих точек.
Б) Найдите угол между прямыми РН и АО, если известно, что АВ=РН.
Решение
PK- высота, медиана и биссектриса равнобедренного треугольника РВС.
ВК=КС
ОК=РК/3 ( медианы в точке пересечения делятся в отношении 2:1, считая от вершины)
OF || PH
F- проекция точки О на плоскость основания.
Из подобия треугольников КОF и КРН
OF=PH/3
КF:КH=1:3
КН=НМ
КF:KM=1:6
FM=5KM/6
Плоскости АОF и КРН пересекаются по прямой OF,
OF||PH и РН не пересекатся с АО.
Б) Пусть АВ=ВС=СD=DA=PH=x.
OF=PH/3=x/3
Из прямоугольного треугольника АFM:
AF^2=AM^2+MF^2=(x/2)^2+(5x/6)^2=(x^2/4)+(25x^2/36)=
=34x^2/36
AF=xsqrt(34)/6
Из прямоугольного треугольника АОF
tg∠AOF=AF/FO=(xsqrt(34)/6)/(x/3)=sqrt(34)/2