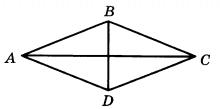
Задача 10969 В ромбе ABCD АС=12; BD=5. Найдите длину...

slava191

28.10.2016

В ромбе ABCD АС=12; BD=5. Найдите длину вектора vector{AD}-vector{BD}

Ответ: 6,5

SOVA

28.10.2016

★

vector{AD}-vector{BD}=vector{AD}+vector{DB}=vector{AB}
|vector{AB}|=a, где а - сторона ромба
По теореме Пифагора
a^2=(AC/2)^2+(BD/2)^2=6^2+(2,5)^=36+6,25=42,25=6,5
О т в е т. |vector{AB}|=6,5