Задача 60197 xy'-y=-y^2(lnx+2)...
Условие
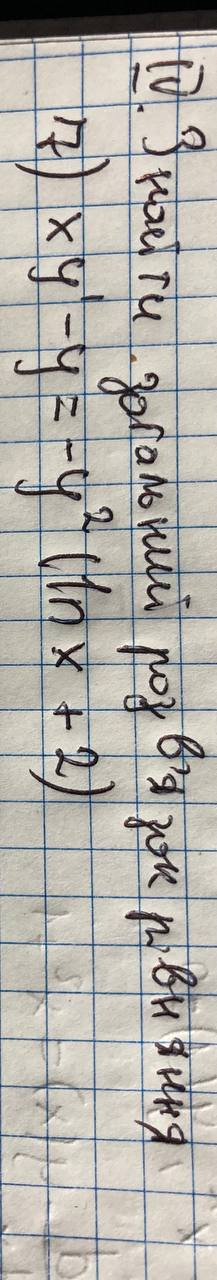
Решение
[m]y`-\frac{1}{x}y=-\frac{lnx+2}{x}\cdot y^2[/m] - уравнение Бернулли
Сводится к линейному уравнению первого порядка
Делим на [m] y^2[/m]
[m]\frac{1}{y^2}\cdot y``-\frac{1}{x}\cdot \frac{1}{y}=-\frac{lnx}{x}-\frac{2}{x}[/m]
Замена: [m]\frac{1}{y}=z[/m] ⇒ [m]-\frac{1}{y^2}\cdot y`=z`[/m]
[m]z`+\frac{1}{x}\cdot z=\frac{lnx}{x}+\frac{2}{x}[/m] [red] (#)[/red]
Решаем методом Бернулли.
Введение двух функций: z(x)=u(x)*v(x)
тогда z`=u`*v+u*v`
Подставляем в линейное уравнение [red](#)[/red]
[m]u`\cdot v+u\cdot v`+\frac{1}{x}\cdot u\cdot v=\frac{lnx}{x}+\frac{2}{x}[/m]
Группировка: [m]u`\cdot v+u\cdot (v`+\frac{1}{x}\cdot v)=\frac{lnx}{x}+\frac{2}{x}[/m]
Полагаем:
[m]( v`+\frac{1}{x}\cdot v)=0[/m]
тогда
[m]u`\cdot v+u\cdot 0=\frac{lnx}{x}+\frac{2}{x}[/m]
Решаем два уравнения с разделяющимися переменными:
[m]( v`+\frac{1}{x}\cdot v)=0[/m] ⇒ [m]\frac{dv}{dx}=-\frac{1}{x}\cdot v[/m] ⇒ [m]\frac{dv}{v}=-\frac{dx}{x}[/m]
Интегрируем: [m] ∫ \frac{dv}{v}=- ∫ \frac{dx}{x}[/m] ⇒ [m]ln|v|=-ln|x| [/m] ( С =0)
[m]v=\frac{1}{x}[/m]
Подставляем во второе уравнение: [m]u`\cdot v+u\cdot 0=\frac{lnx}{x}+\frac{2}{x}[/m]
[m]u`\cdot\frac{1}{x}=\frac{lnx}{x}+\frac{2}{x}[/m] и решаем уравнение с разделяющимися переменными
[m]\frac{du}{dx} \cdot\frac{1}{x}=\frac{lnx}{x}+\frac{2}{x}[/m]
[m]\frac{du}{dx} \cdot\frac{1}{x}=\frac{lnx}{x}+\frac{2}{x}[/m]
[m]du=(lnx+2)dx[/m]
Интегрируем:
[m] ∫ du= ∫ (lnx+2)dx[/m]- интегрируем по частям
[m]u=x\cdot lnx+x + C[/m]
Тогда [m]z=u(x)\cdot v(x)=(xlnx+x+C)\cdot \frac{1}{x}[/m]
[blue][m]z=\frac{xlnx+x+C}{x}[/m][/blue]
Обратная подстановка
[m]y=\frac{1}{z}[/m]
[m]y=\frac{x}{xlnx+x+C}[/m] - о т в е т
при С= ∞ решение y=0 входит в ответ
