Задача 9968 Найти наибольшее и наименьшее значение...
Условие
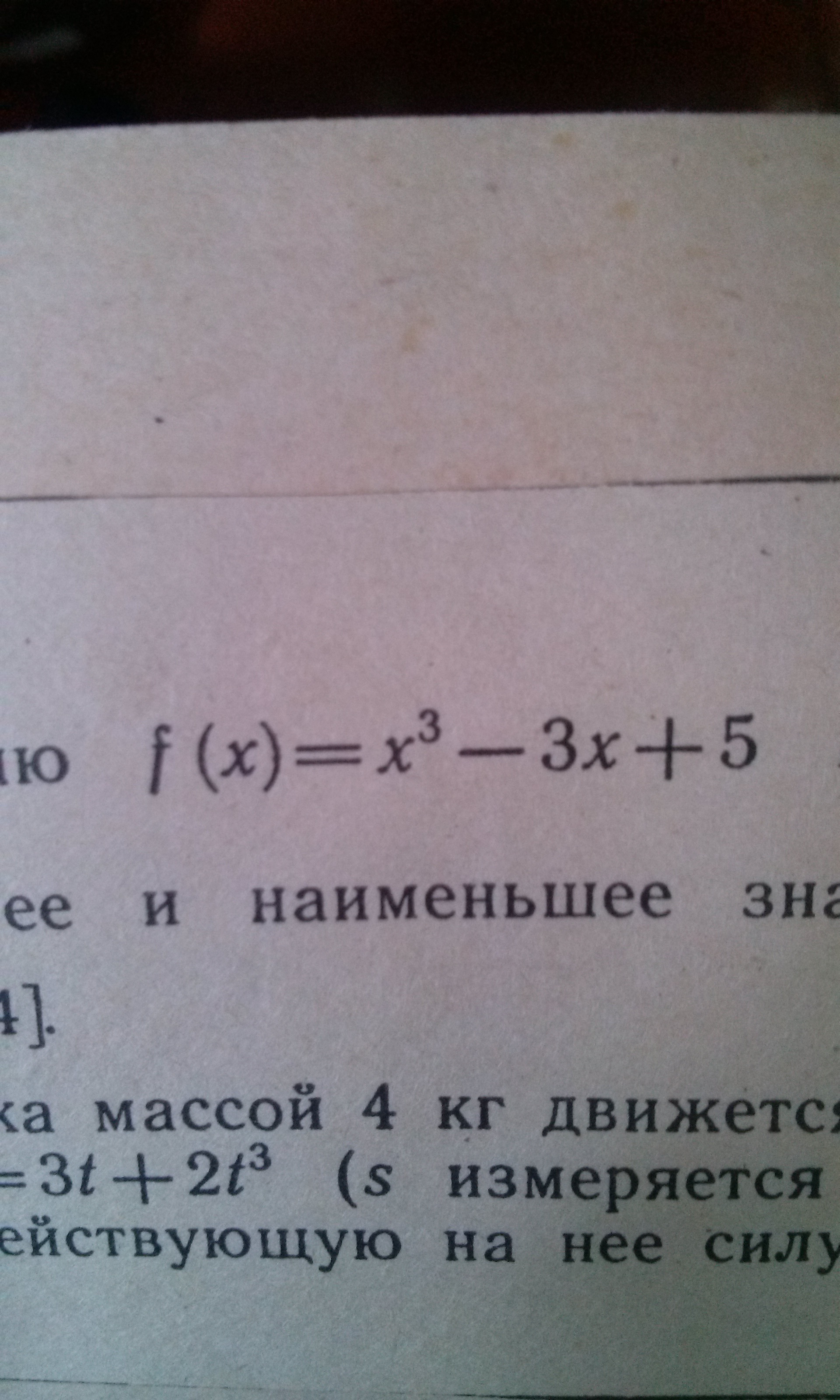
математика 10-11 класс
1916
Решение
★
f`(x)=0;
3x^2-3=0;
3(x^2-1)=0;
x=-1 x=1 - точки возможного экстремума.
Применяем достаточное условие точек экстремума.
Находим знак производной
На (-беск;-1) и на (1;+ беск.) производная положительна. на (-1;1) производная отрицательна.
На (-беск;-1) и на (1;+ беск.) функция возрастает. на (-1;1) функция убывает.
х=-1 точка локального максимума
х=1- точка локального минимума.
f(1)=1-3+5=3
f(-1)=-1+3+5=7