Задача 9905 Решите неравенство...
Условие
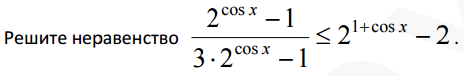
математика 10-11 класс
7579
Решение
★
Неравенство примет вид:
(t-1)/(3t-1) ≤ 2t-2;
(t-1-2(t-1)(3t-1))/(3t-1) ≤ 0;
(t-1)(1-6t+2)/(3t-1) ≤ 0;
(t-1)(3-6t)/(3t-1) ≤ 0;
Решаем методом интервалов.
Находим нули числителя:
t=1; t=1/2.
Находим нули знаменателя
t=1/3
Знаки
на (0; 1/3) +; на (1/3;1/2)-; на (1/2;1)+; на (1;+ бесконечность) -.
Решение неравенства:
1/3 < t ≤1/2 или t ≥ 1
Обратная замена:
1/3 < 2^(cosx) ≤ 1/2 или 2^(cosx) ≥1;
cosx ≤-1 или сosx≥ 0
cosx=-1
x=(-π)+2πk, k ∈ Z. (-π/2)+2πn ≤x ≤(π/2)+2πn, n ∈ Z
О т в е т.(-π)+2πk, k ∈ Z; (-π/2)+2πn ≤x ≤(π/2)+2πn, n ∈ Z.
Все решения
