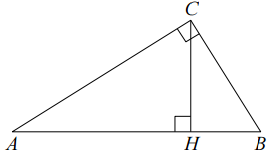
Задача 9793 В треугольнике ABC угол ACB равен 90°,...

slava191

03.09.2016

В треугольнике ABC угол ACB равен 90°, cos A = 0,8, AC = 4. Отрезок CH — высота треугольника ABC (см. рисунок). Найдите длину отрезка AH.

cos A = AC/AB, а значит можно найти AB.

AB = AC/cosA = 4/0,8 = 5

Найдем CB.

СВ^2 = AB^2 - AC^2 (по т. Пифагора)

CB = sqrt(5^2 - 4^2) = sqrt(9) = 3

Мы знаем формулу (называется она Формула длины высоты через стороны):

CH = AC*CB/AB = 4*3/5 = 12/5

Теперь по теореме Пифагора найдем AH.

AH^2 = AC^2 - CH^2

AH = sqrt(4^2 - (12/5)^2) = sqrt(16-144/25) = sqrt((400-144)/25) = sqrt(256/25) = 16/5 = 3,2

Ответ: 3,2

u109165758

17.02.2017

Из треугольника ACH AH=AC COSA.AH=4*0,8=3,2