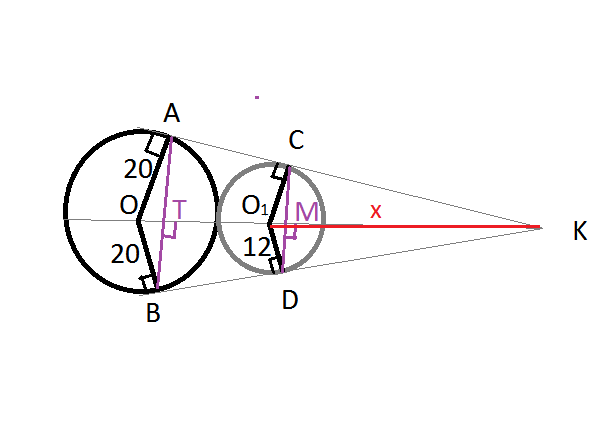
Задача 9683 Окружности радиусов 12 и 20 касаются...

Sana123

13.08.2016

Окружности радиусов 12 и 20 касаются внешним образом. Точки А и В лежат на первой окружности, точки С и D - на второй. При этом АС и BD - общие касательные окружностей. Найдите расстояние между прямыми АВ и CD.

SOVA

13.08.2016

★

ΔОАК подобен ΔО₁СК по двум углам. Один угол общий, второй прямой (касательная перпендикулярна радиусу, проведенному в точку касания.
ОА=R=20;
OC=r=12;
OO₁=R+r=20+12=32;
О₁К=х.
Из подобия следует пропорциональность сторон.
ОА:О₁С=ОК:О₁К;
20:12=(х+32):х;
20x=12x+384;
8x=384;
x=48.
О₁К=48; ОК=48+32=80.

По теореме Пифагора из ΔОАК
АК²=ОК²-ОА²=80²-20²=6400-400=6000;
АК=20√15.
По теореме Пифагора из ΔО₁СК
СК²=О₁К²-ОС²=48²-12²=2304-144=2160;
СК=12√15.
АС=АК-СК=20√15-12√15=8√15.

Диаметр ОО₁ перпендикулярен хорде АВ и хорде CD и делит их пополам.
АТ и СМ - высоты прямоугольных треугольников ΔОАК и ΔО₁СК. Применяем метод площадей. Находим площадь прямоугольного треугольника как половину произведения катетов и как половину произведения основания( гипотенузы) на высоту.
АТ=20•20√15/80=5√15;
СМ=12•12√15/48=3√15;
Рассматриваем прямоугольную трапецию АСМТ:
МТ²=АС²-(АТ-СМ)²=(8√15)²-(5√15-3√15)=64•15-4•15=15•60=900
МТ=30.
О т в е т. Расстояние между прямыми АВ и CD равно 30.