Задача 9649 Найдите все значения параметра a, при...
Условие
Решение
2)x^2+ax+3 ≥ 0.
Оба неравенства должны выполняться одновременно, т.е. фактически это система неравенств.
Возведем обе части уравнения в квадрат, чтобы избавиться от знака радикала.
15x^2+6ax+9=(x^2+ax+3)^2
Сумма трёх членов возводится в квадрат по правилу - все три квадрата и все три удвоенных произведения, т.е.
(a + b + c)^2 = a^2 + b^2 + c^2 + 2ab + 2bc + 2ac.
Либо, с помощью формулы квадрата суммы:
(a + (b + c))^2 = a^2 + 2a(b + c) + (b + c)^2 и далее.
Любым способом после возведения в квадрат получим
15x^2 + 6ax + 9 = x^4 + (ax)^2 + 9 + 2x^2·ax + 2ax·3 + 6x^2
Преобразуем: переносим все слагаемые в правую часть, приводим подобные члены, общий множитель выносим за скобки. Имеем:
x^2·(x^2 + 2ax + a^2 − 9) = 0
Очевидно, что x = 0 будет корнем этого уравнения при любом значении параметра a. Проверим ОДЗ при x = 0.
1) 15·0^2 + 6a·0 + 9 ≥ 0; 9 ≥ 0;
2) 0^2 + a·0 + 3 ≥ 0; 3 ≥ 0.
Оба неравенства выполняются также при любом значении параметра a. Значит один корень уже есть и теперь нам осталось найти все значения параметра a, при каждом из которых квадратное уравнение
x^2 + 2ax + a^2 − 9 = 0
имеет ровно два различных решения, не совпадающих с x = 0 и удовлетворяющих ОДЗ.
Исследуем дискриминант:
D = (2a)^2 − 4·1·(a^2 − 9) = 36 > 0.
Таким образом, последнее уравнение при любом a имеет два разных корня, которые мы можем найти
x1 = (−2a − 6)/2 = −a − 3;
x2 = (−2a + 6)/2 = −a + 3.
Совпадение с первым (нулевым корнем) может быть при −a + 3 = 0; a = 3 и при −a − 3 = 0; a = −3.
Осталось сверить эти корни с ОДЗ исходного уравнения.
Проверяем, подставляя поочередно оба корня в оба неравенства.См. рис.
Итак, первому неравенству всегда удовлетворяют оба корня. Чтобы оба корня удовлетворяли второму неравенству, нужно чтобы параметр a удовлетворял системе условий a ≥ -4 и a ⩽ 4 , т.е. принадлежал промежутку [−4; 4].
Таким образом, a ∈[−4; 4],кроме a = ±3.
Ответ: a ∈[−4;−3)∪(−3; 3)∪(3; 4]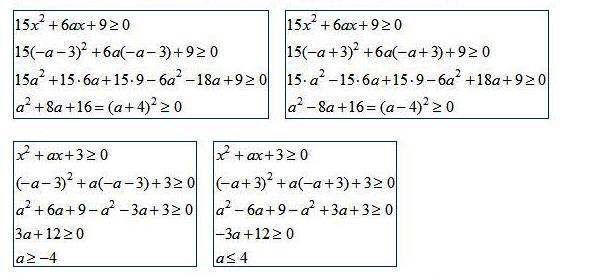
Ответ: [−4;−3)∪(−3; 3)∪(3; 4]