Задача 9647 В трапеции ABCD боковая сторона АВ...

Julia_Trusova

03.08.2016

В трапеции ABCD боковая сторона АВ перпендикулярна основаниям. Из точки А на сторону CD опустили перпендикуляр АН. На стороне АВ отмечена точка Е так, что прямые CD и СЕ перпендикулярны.

а) Докажите, что прямые ВН и ЕD параллельны.

б) Найдите отношение ВН:ED, если угол BCD=135 градусов

а) Продлим боковые стороны трапеции до их пересечения.
АВ⋂CD=O.
Отметим, что ∠ BCE=∠ HAD в силу равенства углов между парами параллельных прямых. Тогда, безусловно, △ BCE ~ △ HAD по двум углам (с учетом наличия прямых углов). Из указанного подобия вытекает, что
BE/HD=EC/AD
так как CE||AH => △OCE ~ △OAD => CE/AD=OE/OD.
Из этих двух пропорций сделаем вывод о том, что BE/HD=OE/OD.

Преобразуем данную пропорцию:
BE/HD=OE/OD
BE/OE=HD/OD
(OE-OB)/OE=(OD-OH)/OD
1-OB/OE=1-OH/OD
OB/OE=OH/OD.

Из последнего равенства (по двум пропорциональным сторонам и углу) заключаем, что △ OCE ~ △ OAD => ∠ OHB=∠ ODE => BH || ED .

б) ∠ BCD=135° => ∠ OCB=45° => △ OBC — равнобедренный. Тогда OB=BC. Аналогичный вывод BC=BE сделаем из равнобедренности прямоугольного треугольника BEC ( ∠ BCD=45^° ). Легко видно, что B — середина OE => k=2 — коэффициент подобия для △ OCE и △ OAD . Следовательно BH:ED=1:2


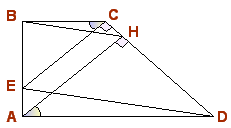
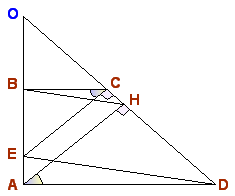
Ответ: 1:2