Условие
Автомобиль, двигаясь по горизонтальной дороге, совершает поворот по дуге окружности. Каков минимальный радиус этой окружности при коэффициенте трения шин автомобиля о дорогу ? = 0,4 при скорости автомобиля v = 10 м/с.
физика 10-11 класс
22299
Решение
Приняв автомобиль за материальную точку, можно утверждать, что она находится под действием сил: силы трения, которая является ньютоновской силой и силой инерции (центробежной силой) которая часто называется фиктивной или не ньютоновской. В проекции на горизонтальную ось уравнение второго закона Ньютона представится в виде:
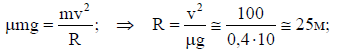
Ответ: 25
Все решения
сила выталкивающая авто =м*10*10/К
сила трения = м*9,81*0,4
m*100/R=4*m
отсюда R=25 м
Написать комментарий