Задача 9490 а) Решите уравнение...

slava191

21.06.2016

а) Решите уравнение 2sin^2x+4=3sqrt(3)sin(3Pi/2+x)
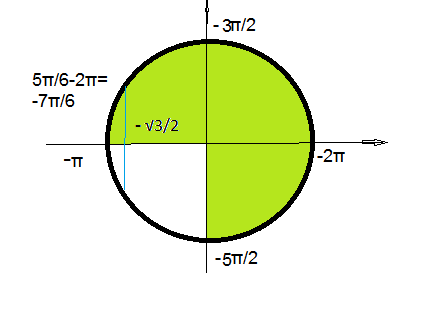
б) Найдите корни этого уравнения, принадлежащие промежутку [-5Pi/2;-Pi]

SOVA

21.06.2016

★

По формулам приведения:
sin(3π/2 + x)= – cosx.
Так как
sin²x = 1 – cos²x, уравнение принимает вид
2•(1 – cos²x)+4 = 3√3•(– cosx)
или
2cos²x – 3√3cosx-6=0
D=(-3√3)²-4•2•(-6)=27+48=75
cosx=(3√3–5√3)/4=–√3/2 или cos x =(3√3+5√3)/4=2√3
x = ± arccos(–√3/2)+2πk, k∈ Z;
x=±(π-arccos(√3/2))+2πk, k∈ Z;
x=±(π-(π/6))+2πk, k∈ Z;
х=± (5π/6)+2πk, k∈ Z.

2√3>1 - второе уравнение не имеет корней.

О т в е т. a) ±(5π/6)+2πk, k∈ Z.

2)Указанному промежутку принадлежит один корень:
х=(5π/6)-2π=-7π/6.
О т в е т. б)-7π/6∈[-5π/2; -π]