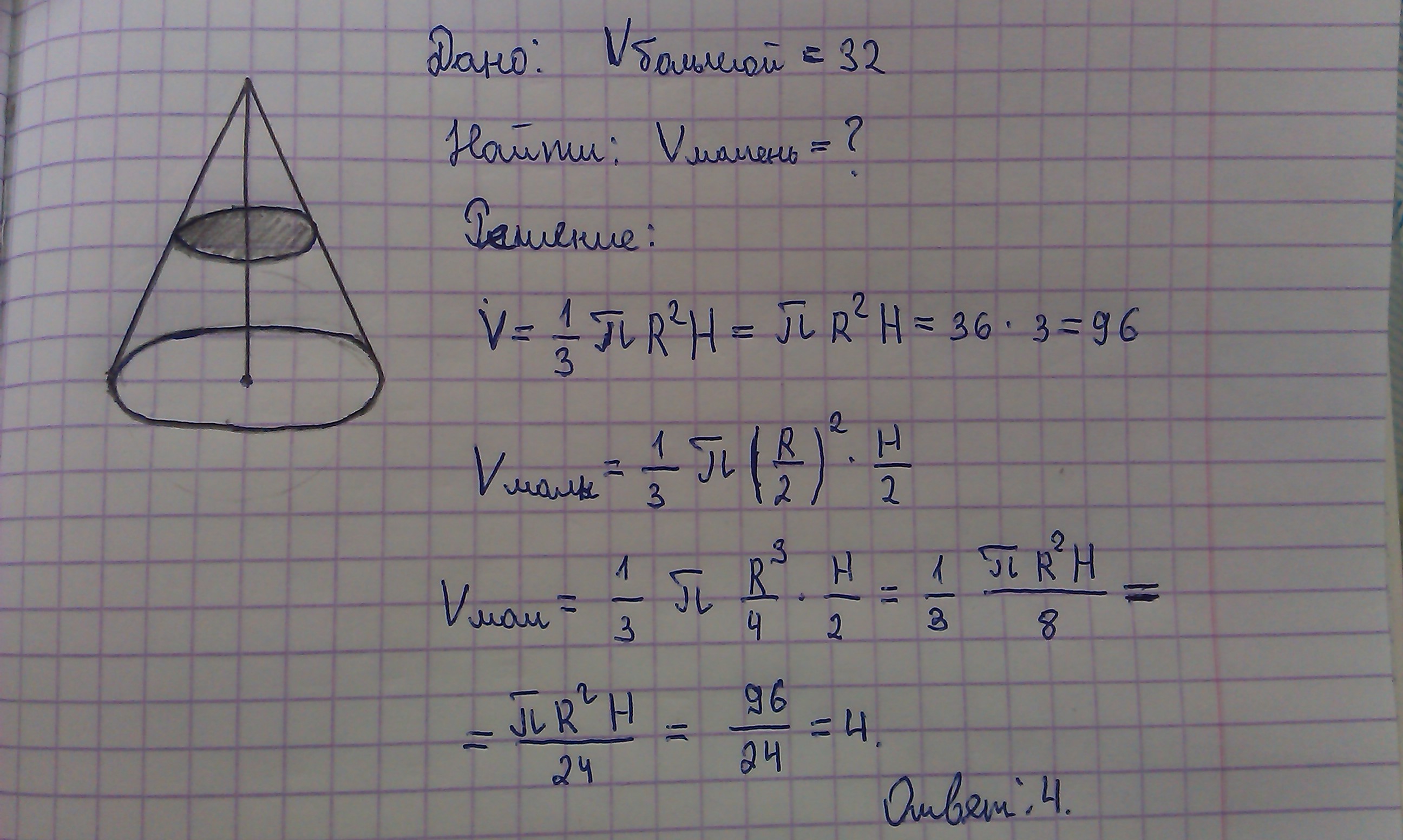Задача 939 объем конуса равен 32. через середину...

Гость

15.04.2014

объем конуса равен 32. через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. найти объем меньшего конусам

slava191

04.03.2017

Формула объема конуса V = (1/3)PiR^2*H

V_(большего конуса) = (1/3)PiR^2*H = 32


V_(меньшего конуса) = (1/3)*Pi*(R/2)^2*H/2 = 1/8 * (1/3)PiR^2*H = 1/8 * V_(большего конуса) = 1/8 * 32 = 4

Ответ: 4