Задача 9184 ...

Julia_Trusova

17.05.2016

Стороны параллелограмма равны 9 и 15. Высота, опущенная на меньшую из этих сторон, равна 10. Найдите высоту, опущенную на бо́льшую сторону параллелограмма.

Из △ ВСЕ по теореме Пифагора:
СЕ=sqrt(15^2-10^2)=sqrt(225-100)=sqrt(125)=5sqrt(5)
DE=9-5sqrt(5)
Из △ ВЕD по теореме Пифагора:
BD=sqrt(10^2+(9-5sqrt(5))^2)=sqrt(100+81-90sqrt(5)+125)=sqrt(306-90sqrt(5))
Пусть ВН=у, АН=х
По теореме Пифагора из △АВН:
y^2+x^2=9^2
y^2=81-x^2
По теореме Пифагора из △ВНD:
y^2+(15-x)^2=(sqrt(306-90sqrt(5)))^2
y^2=306-90sqrt(5)-225+30x-x^2
Таким образом, 81-x^2=306-90sqrt(5)-225+30x-x^2
30x=90sqrt(5)
x=3sqrt(5)

y^2=81-(3sqrt(5))^2
y^2=81-45
y=sqrt(36)=6
BH=6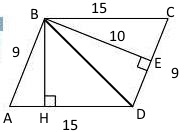

Ответ: 6