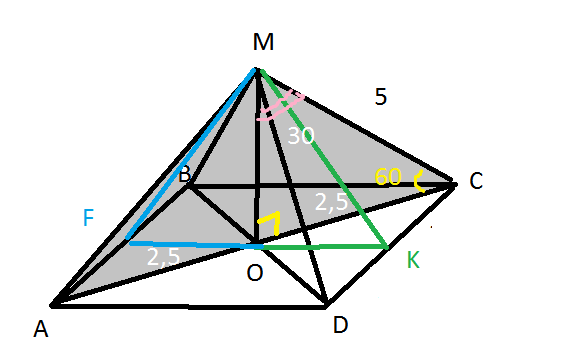
Задача 9062 ...

ViktorSuknev

12.05.2016

В правильной четырехугольной пирамиде MABCD боковое ребро равно 5 и наклонено к пло­скости основания под углом 60°. Найдите:

а) площадь боковой поверхности пирамиды;
б) объем пирамиды;
в) угол между противоположными боковыми гранями;
г) скалярное произведение векторов (MA+MC)∙ME ;
д) площадь описанной около пирамиды сферы;
е) угол между боковым ребром AM и плоскостью DMC

SOVA

12.05.2016

★

В основании пирамиды квадрат АВСD. МО- высота пирамиды. ( см. рис.)
В прямоугольном треугольнике МОС,один острый угол 60°, значит второй острый угол 30°.
Катет, лежащий против угла в 30° равен половине гипотенузы.
Поэтому ОС=2,5; АС=2ОС=5.
АС-диагональ квадрата АВСD, АВ=ВС=СD=AD=5√2/2.
1) площадь боковой поверхности пирамиды
Находим апофему МК из треугольника МКС.
DK=KC=5√2/4; MC=5.
МК²=MC²-KC²=5²-(5√2/4)²=25-(25•2/16)=25•(1-(1/8))=25•(7/8).
MK=5√(7/8).
S(бок)=4•S(Δ MDC)=4•DC•MK/2=4•(5√2/2)•5√(7/8)/2=
=(25√7)/2.

2) объем пирамиды
Из прямоугольного треугольника МОC по теореме Пифагора.
МО²=МC²-ОC²=5²-(5/2)²=75/4.
MO=Н=(5√3)/2.
V(пирамиды)=(1/3)S(осн.)•Н=
=(1/3)•((5√2)/2)²•(5√3)/2=(125√3)/12.

3) Это угол образованный двумя апофемами боковых граней МК и МF и отрезком KF, соединяющим середины противоположных сторон квадрата и равным стороне квадрата.
По теореме косинусов:
KF²=MK²+MF²-2•MK•MF•cosα;
(5√2/2)²=(5√(7/8))²+(5√(7/8))²-
2•5√(7/8)•5√(7/8)•сosα.
cosα=5/7.

4) скалярное произведение векторов (MA+MC)•ME.
Непонятно, где расположена точка Е.
Сумма векторов МА и МС это вектор совпадающий с МО и имеющий длину в два раза больше.

Скалярное произведение векторов 2MO и MЕ равно произведению длин этих векторов на косинус угла между ними.

5) площадь описанной около пирамиды сферы
Найдем радиус сферы. Это радиус окружности, описанной около треугольника АМС.
Треугольник АМС - равносторонний, МА=МС=АС=5.
По формуле
R=abc/4S=(5•5•5)/(4•(5•5•√3/4))=5/√3
S=4πR²=4π•(5/√3)²=100π/3.
6) угол между АМ и плоскостью DMC
это угол между прямой АМ и ее проекцией на плоскость DMC.
Из точки А проводим перпендикуляр к плоскости DMC.
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости.
Этот перпендикуляр есть AD .
AD⊥СD ( стороны квадрата перпендикулярны)
AD⊥МК ( МК⊥СD).
Значит MD - проекция AM.
Угол AMD - между прямой AM и плоскостью MDC.
По теореме косинусов из треугольника AMD:
AD²=AM²+MD²-2•AM•MD•cosβ
(5√2/2)²=(5)²+(5)²-2•5•5•сosβ.
cosβ=3/4.