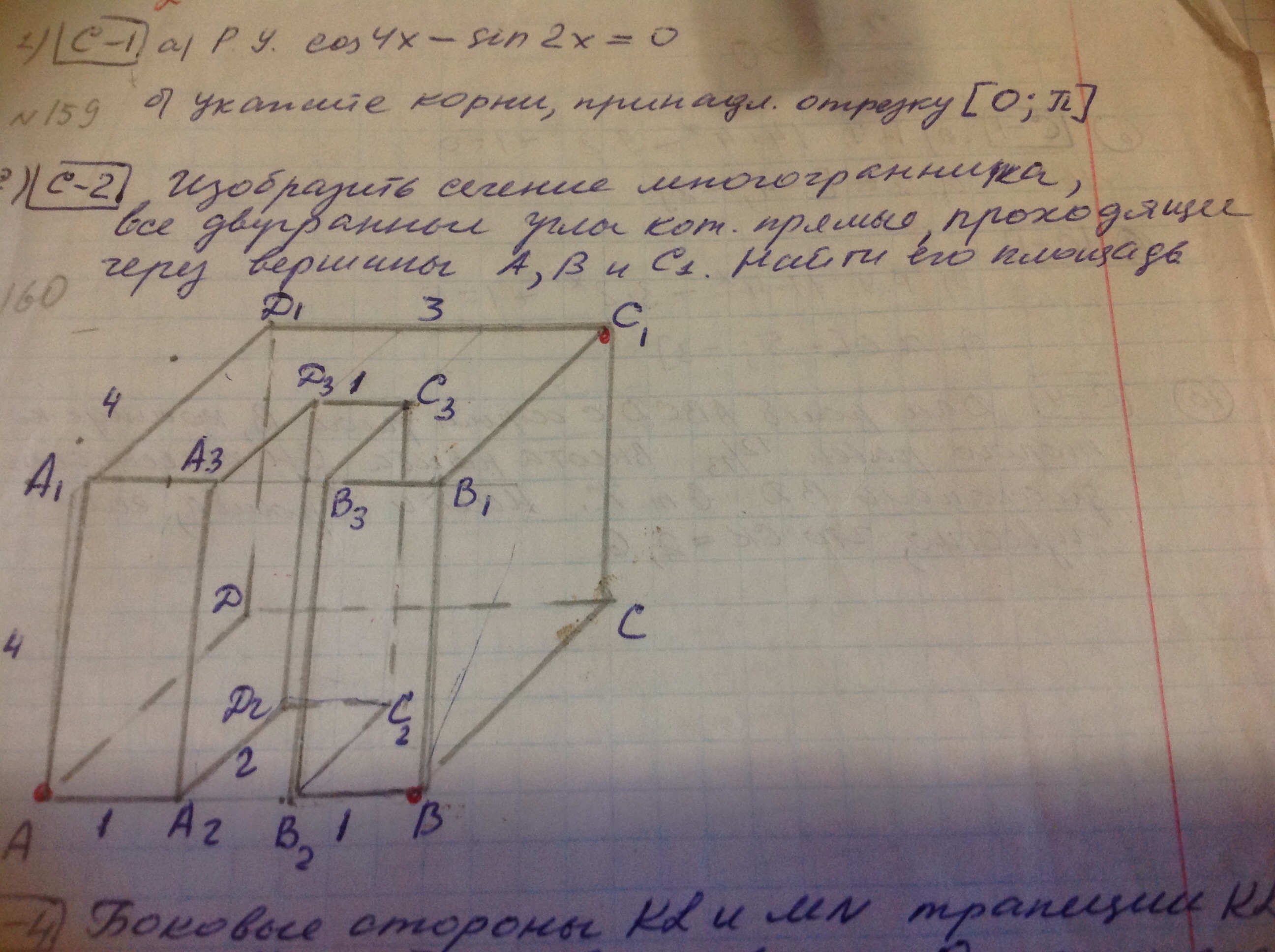
Задача 8972 Изобразить сечение многогранника, все...
Условие
математика 10-11 класс
1913
Решение
★
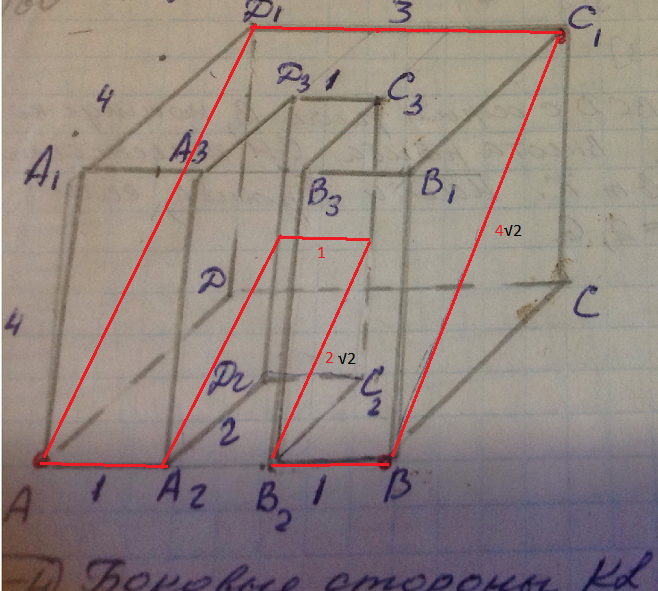
Секущая плоскость пересекает нижнее основание по отрезкам АА₂ и В₂В прямой АВ, а верхнее основание по прямой D₁C₁, параллельной АВ.
ВС₁=4√2.
Проводим через точки А₂ и В₂ прямые параллельные прямым ВС₁ и АD₁.
Отрезки этих прямых при пересечении с D₂D₃ и С₂С₃ обозначим M и N.
MN || АВ и MN ||D₁С₁. MN=1
A₂M=B₂N= 2√2 =(1/2)ВС₁.
S=D₁С₁•ВС₁-MN•A₂M=3•4√2-1•2√2=12√2-2√2=10√2