Задача 8955 Какова вероятность того, что корни...

NikitaEhlakov

08.05.2016

Какова вероятность того, что корни уравнения х^2+ах+с=0 будут разных знаков, если коэффициенты а и с уравнения выбираются наугад из отрезка [-1;3]?

SOVA

09.05.2016

★

Во- первых, чтобы уравнение имело действительные корни необходимо и достаточно, чтобы дискриминант квадратного уравнения D≥0 или a²-4c≥0.
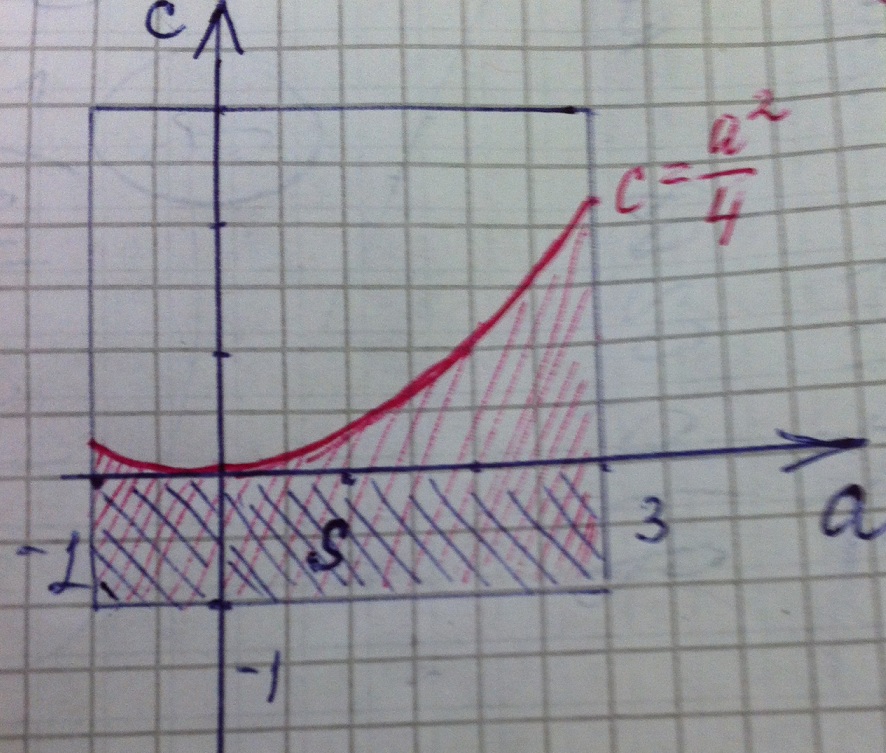
Чтобы применить формулу геометрической вероятности, изобразим область, удовлетворяющую этому неравенству на плоскости аОс.
Граница этой области задается уравнением
a²-4c=0 или с=a²/4.
График- парабола, ветви которой направлены вверх, строим по точкам (-1;1/4);(0;0);(1;1/4);(2;1);(3;9/4).
Так как по условию
-1≤а≤3; -1≤с≤3, то рассматриваем квадрат:
область ограниченную прямыми а=-1; a=3 и
c=-1;c=3.
Неравенству a²-4c≥0 или a²/4≥с удовлетворяет часть квадрата под параболой.
Условие: корни уравнения разных знаков по теореме Виета означает, что с<0.
На плоскости аОс это часть квадрата, расположенная под осью оа.
По формуле геометрической вероятности
р=s/S=4/16=1/4.
S=4•4=16 - площадь квадрата [-1;3] по оси а и [-1;3] по оси с.
s=1•4=4 - площадь прямоугольника, расположенного под осью Оа.
О т в е т. р=0,25.