Задача 8881 ...

Ilya123

04.05.2016

(√2sinx+1)*√(-5cosx)=0- решите уравнение на отрезке [-5П;-7П/2]

SOVA

04.05.2016

★

Произведение двух множителей равно 0, когда хотя бы один из них равен 0, а другой при этом не теряет смысла.
1)√2sinx+1=0 или sin x=-1/√2;
x=-(π/4) + 2πk, k∈Z или x=-(3π/4) + 2πn, n∈Z
При этом (-5 cosx)≥0, cosx≤0.
cos x имеет знак - во 2 и 3 четвертях, значит
х= (-π/4) + 2πn, n∈Z не удовлетворяет условию.
Ответ 1)х= (-3π/4) + 2πk, k∈Z.
или
2)√(–5cosx)=0 или cosx=0;
x= (π/2) + πm, m∈Z.

Ответ 2) x= (π/2) + πm, m∈Z.

Объединяем ответы и получает ответ уравнения

О т в е т. х= -(π/4) + 2πk, k∈Z; х= (π/2) + πm, m∈Z.

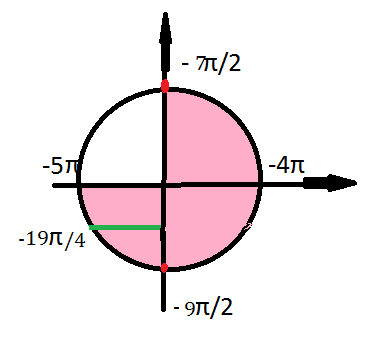
Указанному промежутку принадлежат
(-19π/4); (-7π/2) и (-9π/2)
см. рисунок