Задача 8849 Исследуйте функцию y=x+4/x на...
Условие
Решение
Найдем производную функции
y'=1-4/(x^2)
Найдем критические точки функции, для этого приравняем производную к нулю:
1-4/(x^2)=0
ОДЗ: х≠0
4/(x^2)=1
x^2=4
х1=2, х2=-2
На промежутках от минус бесконечности до -2 и от 2 до плюс бесконечности производная имеет знак плюс, значит функция на этих промежутках возрастает.
На промежутках от -2 до 0 и от 0 до 2 производная имеет знак минус, значит функция на этих промежутках убывает.
Так ка в точке х=-2 производная меняет знак с плюса на минус,х=-2 - максимум функции, а у(-2)=-2+4/(-2)=-4, но не во всей области определения, а в локальном смысле, т.е. по сравнению со значениями функции из некоторой окрестности точки х = -2.
Так как в точке х=2 производная меняет знак с минуса на плюс, то х=2 - минимум функции, а у(2)=2+4/2=4 - наименьшее значение функции, но не во всей области определения, а в локальном смысле, т.е. по сравнению со значениями функции из некоторой окрестности точки х = 2.
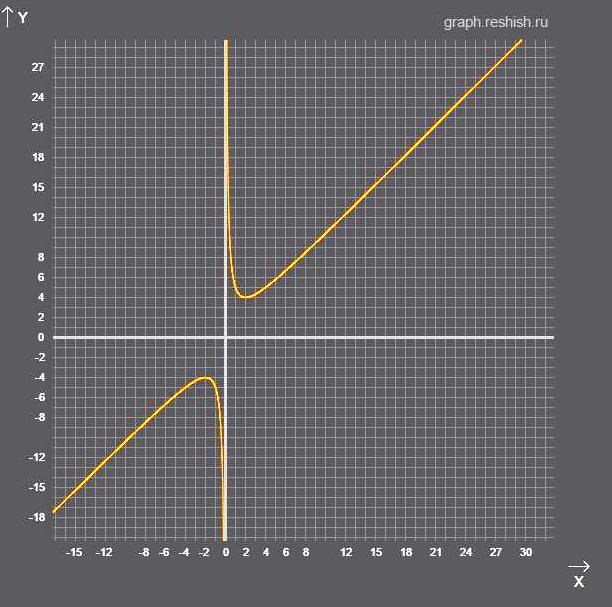
На рисунке представлен график функции
Ответ: В решение