Задача 8821 Биссектрисы углов B и C параллелограмма...
Условие
математика 8-9 класс
30316
Решение
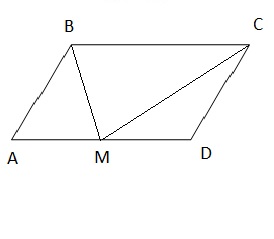
Ответ: В решение

Ответ: В решение