Задача 8726 Дан треугольник АВС со сторонами АВ=5,...

Julia_Trusova

27.04.2016

Дан треугольник АВС со сторонами АВ=5, ВС=9 и АС=10.

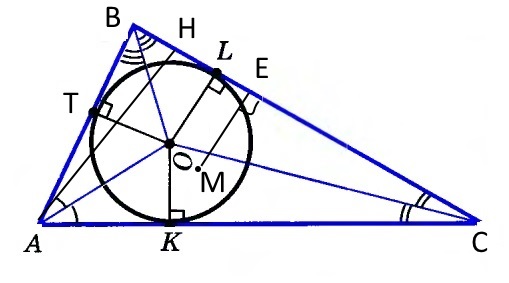
А)Докажите, что прямая, проходящая через точку пересечения медиан и центр вписанной окружности, параллельна стороне ВС.
Б)Найдите биссектрису треугольника АВС , проведенной из вершины А.

А)OL-радиус вписанной окружности
OL=S/p=(2S)/P =(2S)/(5+9+10)=(2S)/24(p-полупериметр, P-периметр)
M-точка пересечения медиан треугольника АВС,
МЕ-расстояние от точки пересечения медиан до стороны ВС
МЕ=1/3*АН, где АН-высота треугольника АВС(АН⊥ВС)
АН=(2S)/BC=(2S)/9 (так как S=1/2*AH*BC)
ME=1/3*(2S)/9=(2S)/27
Таким образом,OL≠ME, значит, прямая ОМ не может быть параллельна ВС.
=>В условии опечатка

Б)Пусть АН=у, ВН=х, тогда НС=9-х

По теореме Пифагора из треугольника АВН:
ВН^2+AH^2=AB^2
x^2+y^2=25
y^2=25-x^2

По теореме Пифагора из треугольника АCН:
AН^2+CH^2=AC^2
y^2+(9-x)^2=100
25-x^2+81-18x+x^2=100
-18x=-6
х=1/3

у=sqrt(25-1/9)=sqrt((224)/9)=4sqrt(14)/3

Значит, АН=4sqrt(14)/3, ВН=1/3, тогда НС=9-1/3=26/3

S(ABC)=1/2*4sqrt(14)/3*9=6sqrt(14)
r=2*6sqrt(14)/24=sqrt(14)/2

Пусть BL=BT=t, LC=CK=9-t, KA=AT=10-(9-t)=10-9+t=1+t, BT=5-(1+t)=5-1-t=4-t
t=4-t
2t=4
t=2
AK=1+2=3

По теореме Пифагора из треугольника АОК:
АО=sqrt(OK^2+AK^2)=sqrt(14/4+9)=sqrt(50/9)=5sqrt(2)/3


Ответ: 5sqrt(2)/3