Задача 8723 В правильной треугольной пирамиде...

Julia_Trusova

27.04.2016

В правильной треугольной пирамиде стороны основания равны 12, а боковые ребра равны 13. Около пирамиды описана сфера.

А)Докажите, что центр сферы лежит на высоте пирамиды.
Б)Найдите расстояние от центра сферы до плоскости основания.

А) Центр сферы лежит на высоте правильной пирамиды или на ее продолжении.(рис.1)

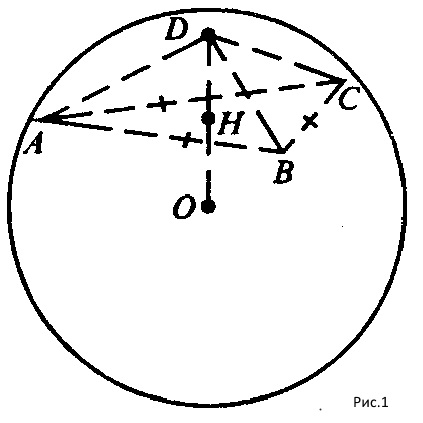
Построим из вершины D пирамиды высоту DH ⊥ плоскости АВС. Проведем отрезки НА, НВ, НС.
ΔDHA=ΔDHB=ΔDHC (они прямоугольные, DH — общий катет, АD=BD=BC — по условию).
НА=НВ=НС=r. r — радиус описанной около ΔАВС окружности.
Проведем отрезок ОG ⊥ плоскости ABC (точка G на рисунке не показана). Проведем отрезки GA, GB, GC, ОА, ОВ, ОС, ΔDCA=ΔOGB=ΔOGC (катет ОG — общий, ОА=ОВ=ОС —R, R — радиус сферы). Значит, GA=GB=GC=r, r — радиус окружности, описанной около AАВС. Следовательно, вокруг ΔАВС можно описать единственную окружность.
Точки Н и G совпадают, и точки D, H, O лежат на одной прямой. Следовательно, центр сферы О лежит на высоте пирамиды DH или на продолжении за точку Н, что и показано на рисунке.

Радиус сферы меньше высоты, значит, цент сферы находится внутри пирамиды(на высоте пирамиды), радиус и высоту найдены ниже.

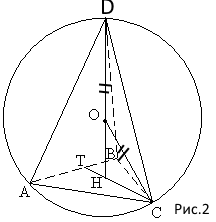
Б)DO=CO=R (рис.2)
СТ-и медиана, и высота основания(треугольника АВС), так как треугольник АВС-правильный
Из треугольника АСТ по теореме Пифагора:
СТ=sqrt(AC^2-AT^2)=sqrt(144-36)=sqrt(108)=6sqrt(3)
CH=2/3CT(по свойству медиан)
СН=2/3*6sqrt(3)= 4sqrt(3)
Из треугольника DHT по теореме Пифагора:
DH=sqrt(DC^2-CH^2)=sqrt(169-48)=sqrt(121)=11
OH=DH-R=11-R
Из треугольника OСH по теореме Пифагора:
OC^2=OH^2+CH^2
R^2=(11-R)^2+48
121-22R+R^2+48-R^2=0
-22R=-169
R=169/22
OH=11-169/22=(242-169)/22=73/22


Ответ: 73/22