Задача 8715 Точка R лежит на стороне AD выпуклого...

fizmat99

26.04.2016

Точка R лежит на стороне AD выпуклого четырёхугольника ABCD, точки А и D являются вершинами равнобедренных треугольников с основаниями BR и CR соответственно, а угол BRC прямой.

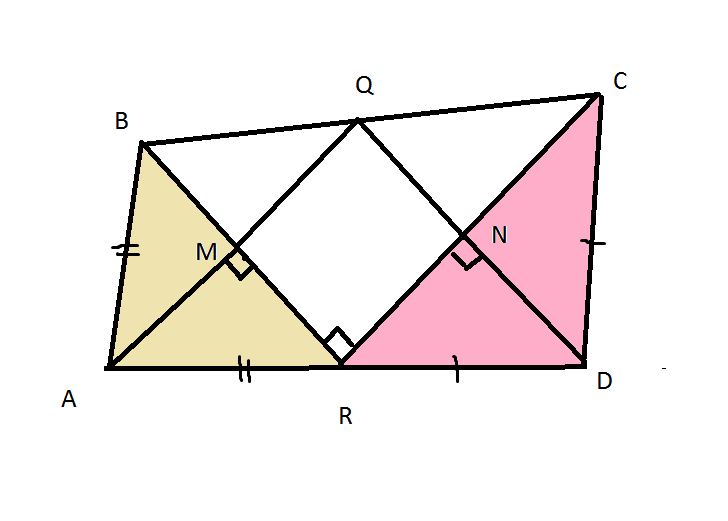
а) Докажите, что биссектрисы углов при вершинах А и D четырёхугольника ABCD пересекаются на стороне ВС.

б) Пусть эти биссектрисы пересекаются в точке Q и DR : RA = 7:3. Найдите площадь четырехугольника ABCD, если площадь четырёхугольника, стороны которого лежат на прямых BR, CR, AQ и DQ, равна 63.

SOVA

27.04.2016

★

1) Треугольник ABR - равнобедренный. АМ - высота, медиана и биссектриса. М - середина ВR.
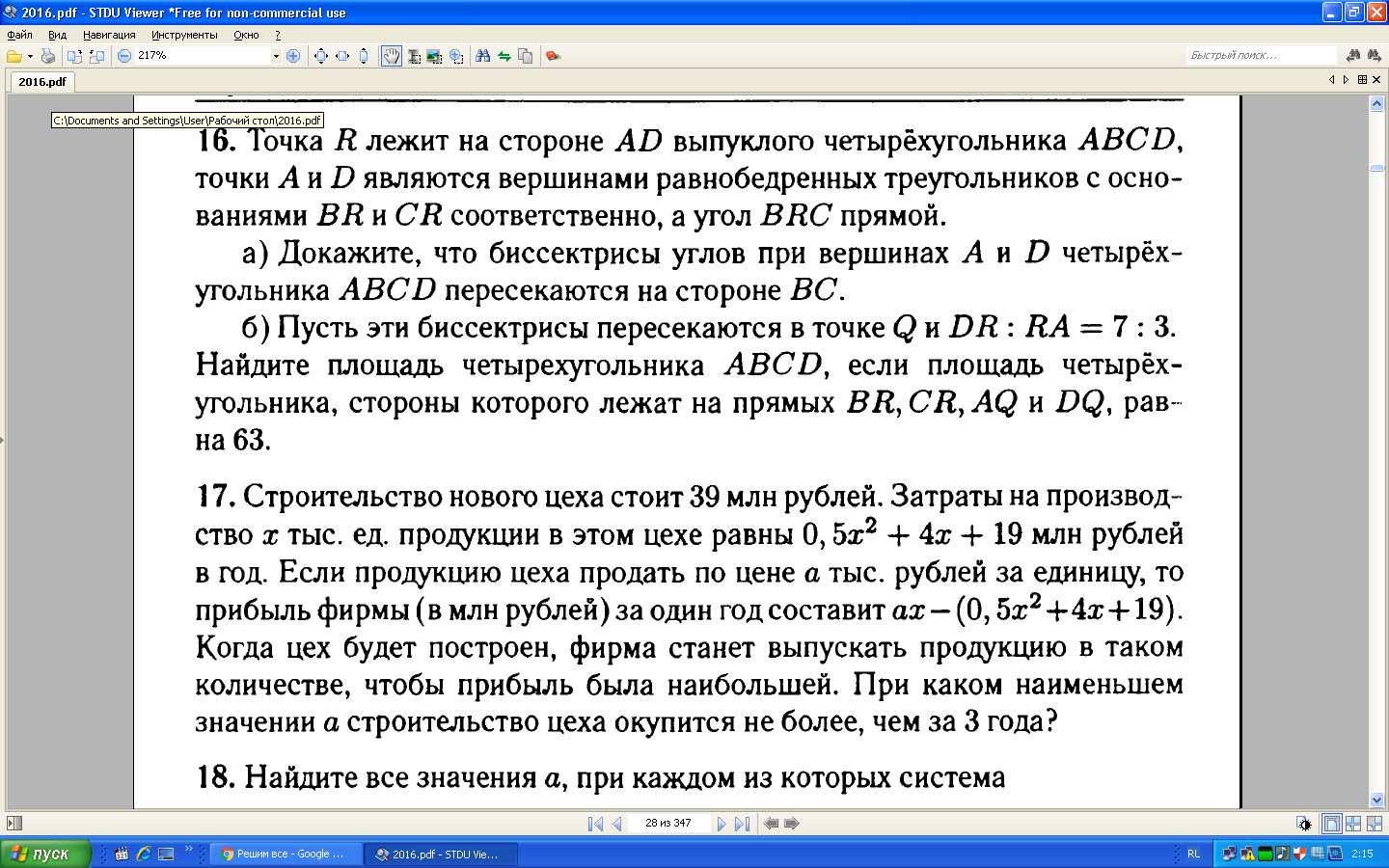
2)Треугольник RCD - равнобедренный. ND - высота, медиана и биссектриса. N - середина RC.
3)RC⊥BR и AM ⊥ BR, значит RC || AM.
MQ- средняя линия треугольника BRC.
BQ=QC=QR.
Треугольник RQC-равнобедренный.
QN⊥RC.
из точки N к RC проведены перпендикуляры QN и ND.
Чего быть не может, значит это один перпендикуляр QD.
Биссектрисы углов A и D - прямые АМ и ND пересекаются в точке Q.
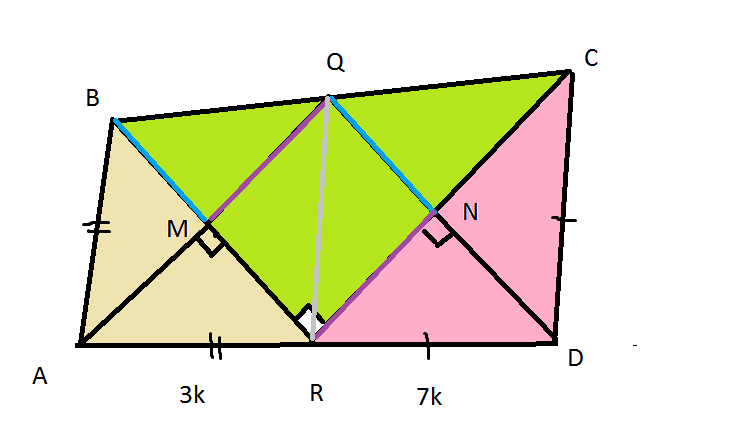
4)MPNQ- прямоугольник, три угла прямые. См. рисунок.
Пусть RN=x, MR=y.
xy=63.
5) Треугольники BMQ и MQR равны по двум катетам, значит и их площади равны.
Треугольники RQN и NQC равны по двум катетам, значит и их площади равны.
S (Δ BRC) =2•63=126 кв.ед.
6)По т. Фалеса
QN:ND=3:7, откуда ND=7QN/3=7y/3.
По т. Фалеса
AM:MQ=3:7, откуда AM=3MQ/7=3x/7.
S(Δ ABR)=BR•AM/2=2BM•AM/2=
=y•3x/7=3xy/7=3•63/7=27 кв.ед.
S(Δ RCD)=RC•ND/2=2RN•ND/2=x•7y/3=
=7xy/3=7•63/3=147 кв.ед.

S(четырехугольника ABCD)= S(Δ BRC)+S(Δ ABR)+
S(Δ RCD)=126+27+147=300 кв. ед.
О т в е т. 300 кв. ед.