Задача 8675 В треугольнике ABC на его медиане BM...

larisashakirova

25.04.2016

В треугольнике ABC на его медиане BM отмечена точка K так, что BK:KM = 4:1. Прямая AK пересекает сторону BC в точке P. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.

Проведём построения как показано на рисунке. Пусть площадь треугольника АВС равна S. Медиана делит треугольник на два равновеликих треугольника, значит S ABM = S BMC =1/2S ABC=S/2. У треугольников ABK и AKM можно провести общую высоту h, тогда S ABK/S AKM=(1/2h•BK)/(1/2h•KM)=BK/KM=4/1=4 => S ABK=4/5•(S ABC/2)=2/5S, S AKM=1/5•(S ADC/2)=1/10S. Аналогично треугольники AKM и КМС имеют одну высоту, откуда S AKM=S KMC=S/10. S BKC=S BMC-S KMC=S/2-S/10=2/5S.
Проведем прямую MNǁAP, KPǁMN => KP-средняя линия => PN=CN. Рассмотрим треугольники ВКР и ВМN: угол МВС - общий, углы ВКР и ВМN равны как соответственные углы при параллельных прямых, откуда: ВМ/ВК=ВN/BP => (BK+KM)/BK=(BP+PN)/BP => 1+KM/BK=1+(BP+PN)/BP => KM/BK=PN/BP=1/4. Аналогично рассмотренным выше случаям S BKP/S KPC=BP/PC=BP/2PN=2. Следовательно, S BKC=3S KPC. S BKC=2/5S => 3S KPC=2/5S => S KPC=2/15S.
S ABK/S KPMC=S ABK/(S KMC+S KPC)=2/5S/(2/15S+1/10S)=2/5•30/(4+3)=12/7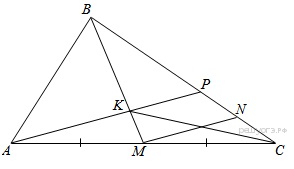

Ответ: 12/7