Задача 8628 В правильной треугольной призме...

Julia_Trusova

23.04.2016

В правильной треугольной призме АВСА1В1С1 стороны основания равны 4, боковые ребра равны 7, точка D-середина ребра ВВ1.

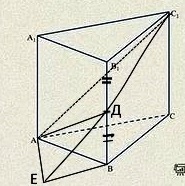
а) Пусть прямые С1D и ВС пересекаются в точке Е. Докажите, что угол ЕАС – прямой.
б) Найдите угол между плоскостями АВС и АDС1.

а) Угол АВЕ=180-60=120 градусов(как смежные)
Треугольник СЕС1 подобен треугольнику ВЕD(по двум углам)
=>ВD/СС1=ВЕ/СЕ=1/2
=>ЕВ=ВС
=>ВЕ=АВ
Тогда треугольник АВЕ – равнобедренный
Угол ВАЕ=углу ВЕА= (180-120):2=30 градусов
Угол ЕАС=30+60=90 градусов. Ч.т.д.

б) Угол между плоскостями АВС и АDС1 это угол между плоскостью АEС и плоскостью ЕАС1
АЕ-общая прямая
АС ⊥ АЕ
АС1 ⊥ АЕ (по теореме о трех перпендикулярах)
=>Угол С1АС – линейный угол двугранного угла между плоскостями АВС и ЕАС1
tg∠C1AC=C1C/AC=7/4=1,75
∠C1AC=arctg1,75


Ответ: arctg1,75