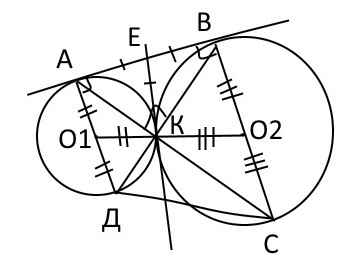
Задача 8618 Две окружности касаются внешним образом...
Условие
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника DКС, если известно, что радиусы окружностей равны 4 и 9.
Решение
Окружность с центром О₂ касается прямой в точке В, радиус окружности О₂В=О₂К.
Через точку К проведем общую касательную к 2 окружностям, которая пересекает АВ в точке Е.
а) Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.
Значит АЕ=ЕК и ВЕ=ЕК, тогда АЕ=ВЕ.
Получается, что ЕК - медиана ΔАВК и ЕК=АВ/2, значит ΔАВК прямоугольный (угол АКВ - прямой)
Следовательно, прямые ВД и АС пересекаются под прямым углом, значит вписанные <АКД=<ВКС=90°. А т.к. вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр, то значит АД и ВС - это диаметры окружностей.
Касательная перпендикулярна к радиусу окружности, проведённому в точку касания, тогда АД ⊥АВ, ВС⊥АВ.
Значит АД || ВС (две прямые, перпендикулярные третьей прямой, параллельны), ч.т.д.
б) По условию радиус окружности О₁А=О₁К=4, а радиус окружности О₂В=О₂К=9.
Диаметры АД=8, ВС=18
Прямоугольные ΔАКД и ΔСКВ подобны по острому углу (<ДАК=<ВСК как накрест лежащие при пересечении параллельных прямых АД и ВС секущей АС).
Значит АК/КС=ДК/КВ=АД/ВС=8/18=4/9
ДК/КВ=АД/ВС=8/18=4/9
КВ=(9ДК)/4
Из прямоугольного ΔДАВ, в котором АК - высота из прямого угла на гипотенузу ВД:
АК²=ДК*КВ=ДК*(9ДК)/4=(9ДК²)/4
АК=(3ДК)/2
Из прямоугольного ΔДАК:
АД²=ДК²+АК²
АД²=ДК²+9ДК²/4=13ДК²/4
ДК=2АД/sqrt(13)==2*8/sqrt(13)=16/sqrt(13)
АК=(3*16/sqrt(13))/2=24/sqrt(13)
КС==(9AК)/4==(9*24/sqrt(13))/4=54/sqrt(13)
Площадь Sдкc=1/2*КД*КС=1/2*16/sqrt(13)* 54/sqrt(13)=432/13
Ответ: 432/13
Ответ: 432/13