Задача 8525 ...

Julia_Trusova

14.04.2016

Около окружности с центром О описана трапеция ABCD с основаниями AD и BC.

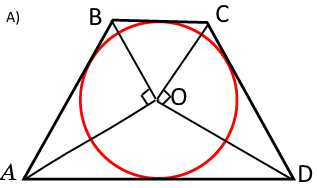
А)Докажите, что ∠ВОС+∠AOD=180°
Б)Найдите отношение оснований трапеции, если известно, что АВ=CD, а площадь четырехугольника с вершинами в точках касания окружности со сторонами трапеции составляет 8/25 площади трапеции ABCD.

А)ВО, АО-биссектрисы, => ∠ВОA=90°
CО, DО-биссектрисы, => ∠CОD=90°
Значит, ∠ВОС+∠AOD=360°-90°-90°=180°

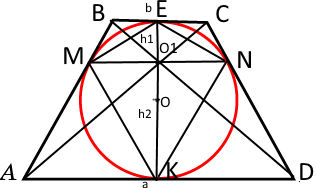
Б) Диагональ трапеции проходит через середину отрезка, концы которого – точки касания окружности с боковыми сторонами трапеции(так как трапеция равнобедренная).
Пусть AD=a, BC=b, EO1=h1, O1K=h2
ΔВО1С~ΔАО1D
=> b/a=h1/h2
=> h1=(b*h2)/a


Ответ: 4:1