Задача 8509 Правильная четырёхугольная пирамида...

Festrou

12.04.2016

Правильная четырёхугольная пирамида SABCD, каждое ребро которой равно 2, расположена внутри цилиндра таким образом, что стороны АВ и CD основания являются образуюшими цилиндра, а вершина 5 — серединой образующей PQ. Найдите объём цилиндра.

SOVA

12.04.2016

★

См. рисунок.
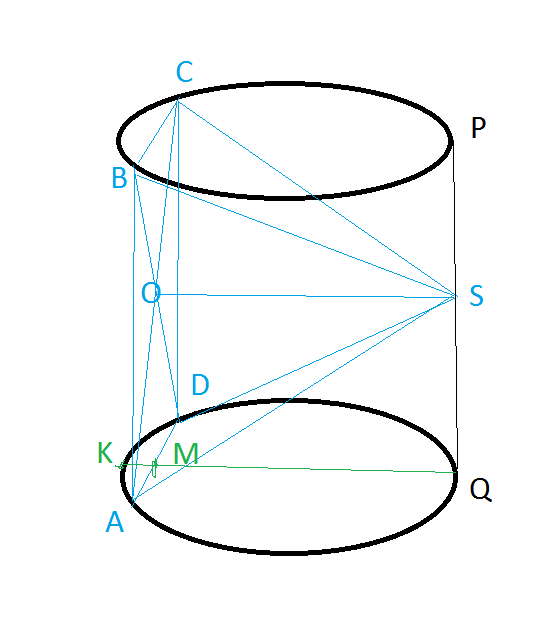
АВСD- квадрат, АВ=ВС=СD=AD=2
O-центр квадрата, точка пересечения диагоналей.
PS=SQ=1
PQ=2- образующая цилиндра и высота цилиндра Н.
Осталось найти радиус основания цилиндра.
Найдем диаметр, это отрезок КQ. (!)
Из соображений проектирования. Равные отрезки имеют равные проекции. Проекцией ВС является AD. Точка О проектируется в центр СD- проекция точка О-точка М.
Причем MQ=SO=h(пирамиды). По теореме Пифагора из треугольника SOC
SO²=SC²-OC²=2²-(√2)²=2 ( АС=2√2- диагональ квадрата со стороной 2, ОС=АС/2).

SO=√2.
По свойству пересекающихся хорд (AM=MD- диаметр, перпендикулярный хорде, делит хорду пополам)
AM•MD=KM•MQ

1•1=KM•(√2)
КM=1:(√2)=√2/2

KQ=KM+MQ=(√2/2)+(√2)=3√2/2

R=КQ/2=3√2/4

V(цилиндра)=π•R²•H=π•(3√2/4)²•2=9π/4 куб ед.