Задача 8490 Биссектриса угла С трапеции ABCD...

Julia_Trusova

11.04.2016

Биссектриса угла С трапеции ABCD пересекает основание AD в точке М.

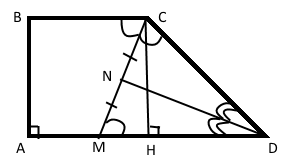
а) Докажите, что биссектриса угла D проходит через середину отрезка СМ.

б) Найдите отношение оснований трапеции, если сторона AD
перпендикулярна стороне АВ и известно, что AM:MD = 1:2 и АВ:CD = 4:5.

а) DN-биссектриса ∠CDM, CM⋂DN=N
∠BCM=∠MCD(CM-биссектриса)
∠BCM=∠CMD как соответственные
=>△CDM-равнобедренный с основанием СМ
Значит,DN является и биссектрисой и медианой
=> CN=MN

б)AM:MD = 1:2
Пусть АМ=х, MD=2x
АВ:CD = 4:5
Пусть AB=4y, CD=5y
CD=MD(△CDM-равнобедренный)
Т.о. 5y=2х
y=2/5x
AB=4*2/5x=8/5x
CH⊥AD
AB=CH=8/5x
Из △CHD по теореме Пифагора:
HD=sqrt(CD^2-CH^2)=sqrt((2x)^2-(8/5x)^2)=sqrt(4x^2-64/25x^2)=sqrt(36/25x^2)=6/5x
BC=AH=3x-6/5x=9/5x
BC:AD=9/5x:3x=3/5


Ответ: 3/5