Задача 8484 Решите неравенство 5^(2/x)+4 >...

Julia_Trusova

10.04.2016

Решите неравенство 5^(2/x)+4 > 5^((1+x)/x)

5^(2/x)+4>5^((1+x)/x)
ОДЗ:х≠0
5^(2/x)+4-5^((1+x)/x)>0
(5^(1/x))^2+4-5^(1/x+x/x)>0
(5^(1/x))^2+4-5^(1/x)*5>0
Замена 5^(1/x)=t, t>0
t^2-5t+4>0
t^2-5t+4=0
D=25-16=9
t1=(5+3)/2=4
t2=(5-3)/2=1
tЄ(0;1)∪(4;+∞)

1)5^(1/x)>0
при любом х
2)5^(1/x)<1
1/x<0
x<0
3)5^(1/x)>4
1/x>log5(4)
x>1/(log5(4))
Ответ:(-∞;0), (1/(log5(4));+∞)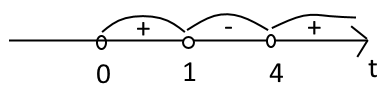

Ответ: (-∞;0), (1/(log5(4));+∞)